题目内容
6．
如图，在△ABC中，∠B=40°，∠C=50°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 90° |
分析 先根据三角形内角和定理计算出∠BAC=180°-∠B-∠C=90°，再根据角平分线的定义得到∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°，然后根据平行线的性质即可得到结论．
解答 解：∵∠B=40°，∠C=50°，
∴∠BAC=180°-∠B-∠C=90°，
∵AD平分∠BAC，
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°，
∵DE∥AB，
∴∠ADE=∠DAB=45°，
故选B．
点评 本题考查了三角形内角和定理：三角形内角和是180°．也考查了平行线的性质．
练习册系列答案
相关题目
17．已知：a=0.5，b=3.2，c=16，d=2.5，下列各式中，正确的是（ ）
| A． | $\frac{a}{b}$=$\frac{c}{d}$ | B． | $\frac{a}{c}$=$\frac{d}{b}$ | C． | $\frac{a}{b}$=$\frac{d}{c}$ | D． | $\frac{d}{c}$=$\frac{b}{a}$ |
14．用火柴摆金鱼如图所示，按照如图的规律摆第n个金鱼需用火柴棒的根数为（ ）
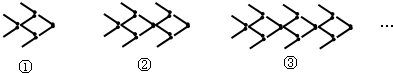
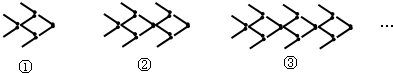
| A． | 8n | B． | 6n | C． | 7n+1 | D． | 2+6n |
11．下列条件中，不能判定△ABC是直角三角形的是（ ）
| A． | ∠A：∠B：∠C=3：4：5 | B． | ∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C | C． | ∠B=50°，∠C=40° | D． | a=5，b=12，c=13 |
15．下午4点30分，时针与分针夹角为（ ）度．
| A． | 75 | B． | 60 | C． | 45 | D． | 30 |