题目内容
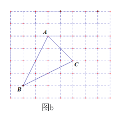
【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).
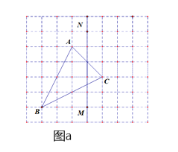
(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
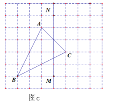
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析,理由见解析.
【解析】
(1)根据轴对称的性质及方格的特点,分别作出A、B、C关于直线MN的对称点![]() ,再顺次连接即可;
,再顺次连接即可;
(2)根据方格的特点,利用三角形面积公式把面积分三等份即可;
(3)根据方格的特点以及全等三角形的判定和性质,利用线段垂直平分线的定义求解.
(1)如图,△A′B′C′为所求作;

(2)如图,取格点O,计算可知S△AOC=S△BOC=S△AOB=2(平方单位)
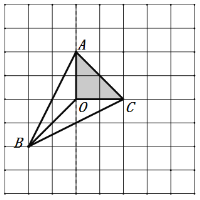
(3)如图,选择格点D、E,证明△ABD≌△CBE.于是,AB=CB.
选择格点Q,证明△ABQ≌△CBQ,于是,AQ=CQ.
∴BQ为线段AC的垂直平分线,
设BQ与AC相交于点F,则BF为所要求的△ABC的边AC上的高.


练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目