题目内容
【题目】观察发现:如图(1),![]() 是
是![]() 的外接圆,点
的外接圆,点![]() 是边
是边![]() 上的一点,且
上的一点,且![]() 是等边三角形.
是等边三角形.![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为圆心、
为圆心、![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)![]() _____;
_____;
(2)线段![]() 、
、![]() 有何大小关系?证明你的猜想.
有何大小关系?证明你的猜想.
拓展应用:如图(2),![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 延长线上的一点.点
延长线上的一点.点![]() 是
是![]() 的外接圆圆心,
的外接圆圆心,![]() 与
与![]() 相交于点
相交于点![]() .如果等边三角形
.如果等边三角形![]() 的边长为2,请直接写出
的边长为2,请直接写出![]() 的最小值和此时
的最小值和此时![]() 的度数.
的度数.

【答案】(1)120°;(2)见解析;(3)拓展应用:![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.
【解析】
(1)根据△ABC是等边三角形,可得∠ACB=60°,根据圆周角定理可得∠AOD的度数.(2)根据内角和定理和等边三角形的性质可得![]() ,进而得到
,进而得到![]() ,根据边角边对应相等可得
,根据边角边对应相等可得![]() ,则
,则![]() .
.
拓展应用:以![]() 为圆心,以
为圆心,以![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() .当
.当![]() 时
时![]() 最小,
最小,![]() 时,
时,![]() .
.
解:观察发现:(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠AOD=2∠ACB=120°
故答案为120°.
(2)结论:AE=CF.
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
拓展应用:以![]() 为圆心,以
为圆心,以![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() ,连结
,连结![]() ,则由以上结论可得:
,则由以上结论可得:![]() .
.
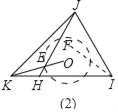
当![]() 时
时![]() 最小,
最小,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目