题目内容
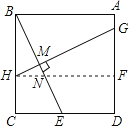
【题目】如图所示，在正方形ABCD中，E为CD的中点，作BE的中垂线GH，垂足为M，则GM：MH的值为（ ）
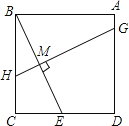
A．4：1 B．3：1 C．3：2 D．5：2
【答案】B
【解析】
试题分析：根据正方形的性质结合全等三角形的判定方法得出△BCE≌△HFG（ASA），则BE=HG，再推出△BHM∽△BEC，进而利用相似三角形的性质得出答案．
解：过点H作HF⊥AD于点F，交BE于点N，
由题意可得：∠BHM+∠GHF=90°，
∠HBM+∠BHM=90°，
则∠CBE=∠GHF，
在△BCE和△HFG中，
，
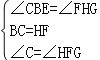∴△BCE≌△HFG（ASA），
∴BE=HG，
∵∠BMH=∠C，∠CBE=∠MBH，
∴△BHM∽△BEC，
∵E为CD的中点，
∴
=
=
，
设HM=x，则BM=2x，故BE=HG=4x，
则MG=4x﹣x=3x，
故GM：MH的值为：3：1．
故选：B．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
