题目内容
【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
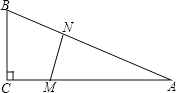
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
【答案】(1)当t为4时,∠AMN=∠ANM.(2)当t=6时,S最大值=![]() 平方米.
平方米.
【解析】
试题分析:(1)用t表示出AM和AN的值,根据AM=AN,得到关于t的方程求得t值即可;
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可.
解:(1)∵从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
∴AM=12﹣t,AN=2t
∵∠AMN=∠ANM
∴AM=AN,从而12﹣t=2t
解得:t=4 秒,
∴当t为4时,∠AMN=∠ANM.
(2)在Rt△ABC中
∵AB2=BC2+AC2
∴AB=13米
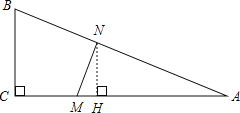
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
∴NH=![]()
从而有S△AMN=![]() (12﹣t)
(12﹣t)![]() =﹣
=﹣![]() t2+
t2+![]() ,
,
∴当t=6时,S最大值=![]() 平方米.
平方米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目