题目内容
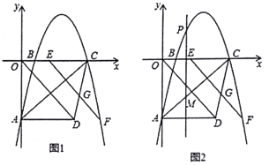
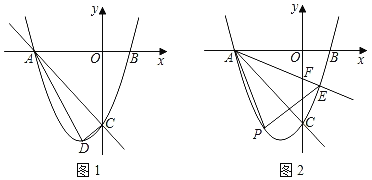
【题目】如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.
(1)求抛物线的解析式;
(2)点D是抛物线顶点,求△ACD的面积;
(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S△ABE=![]() ,求△APE面积的最大值和此动点P的坐标.
,求△APE面积的最大值和此动点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)3;(3)P的坐标为(﹣![]() ,﹣
,﹣![]() )
)
【解析】
(1)先求出点C的坐标,再根据待定系数法即可得出答案;
(2)根据(1)中求出的函数解析式得出点A、C和D的坐标,再利用割补法即可得出答案;
(3)设点E的纵坐标为t,根据△ABE的面积求出t的值,再代入函数解析式即可得出点E的坐标,将A和E的坐标代入即可得出直线AE的解析式,接着根据S△APE=S△APG+S△PEG求出面积的函数关系式,再化为顶点式即可得出答案.
解:(1)∵抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC,
∴a+2a+c=0,点C的坐标为(0,c),
∴点A的坐标为(c,0),
∴ac2+2ac+c=0,
∴![]() ,
,
解得,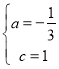 或
或![]() ,
,
∵函数图象开口向上,
∴a>0,
∴a=1,c=﹣3,
∴抛物线的解析式为y=x2+2x﹣3;
(2)∵y=x2+2x﹣3=(x+1)2﹣4,抛物线与与y轴交于点C,顶点为D,OA=OC,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,
∴点D的坐标为(﹣1,﹣4),点C的坐标为(0,﹣3),点A的坐标为(﹣3,0),
连接OD,如右图1所示,
由图可知:
S△ACD=S△OAD+S△OCD﹣S△OAC
=![]()
=3;
(3)∵A(﹣3,0),点B(1,0),
∴AB=4,
设点E的纵坐标为t,t<0,
∵S△ABE=![]() ,
,
∴![]() ,得t=
,得t=![]() ,
,
把y=![]() 代入y=x2+2x﹣3,得
代入y=x2+2x﹣3,得
![]() =x2+2x﹣3,
=x2+2x﹣3,
解得,x1=![]() ,x2=
,x2=![]() ,
,
∵点E在y轴的右侧,
∴点E(![]() ,
,![]() ),
),
设直线AE的解析式为y=mx+n(m≠0),
∴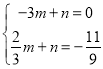 ,得
,得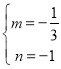 ,
,
∴直线AE的解析式为y=![]() x﹣1,
x﹣1,
过点P作y轴的平行线交AC于点G,如图2所示,
设点P的横坐标为x,则P(x,x2+2x﹣3),点G(x,![]() x﹣1),
x﹣1),
∴PG=(![]() x﹣1)﹣(x2+2x﹣3)=﹣x2﹣
x﹣1)﹣(x2+2x﹣3)=﹣x2﹣![]() x+2,
x+2,
又∵A(﹣3,0),E(![]() ,
,![]() ),
),
∴S△APE=S△APG+S△PEG
=![]()
=![]()
=![]() ,
,
∴当x=﹣![]() 时,S△APE取得最大值,最大值是
时,S△APE取得最大值,最大值是![]() ,
,
把x=﹣![]() 代入y=x2+2x﹣3,得
代入y=x2+2x﹣3,得
y=(﹣![]() )2+2×(﹣
)2+2×(﹣![]() )﹣3=﹣
)﹣3=﹣![]() ,
,
∴此时点P的坐标为(﹣![]() ,﹣
,﹣![]() ).
).



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案