题目内容
【题目】为了加强对校内外安全监控，创建平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格，有效监控半径如表所示，经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．
甲型 | 乙型 | |
价格（元/台） | a | b |
有效半径（米/台） | 150 | 100 |
（1）求a、b的值；
（2）若购买该批设备的资金不超过11000元，且要求监控半径覆盖范围不低于1600米，两种型号的设备均要至少买一台，请你为学校设计购买方案，并计算最低购买费用．
【答案】（1）a=850，b=700；（2）最省钱的购买方案为：购甲型设备2台，乙型设备13台．
【解析】
（1）根据购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元，可列出方程组，解之即可得到a、b的值；
（2）可设购买甲型设备x台，则购买乙型设备（15﹣x）台，根据购买该批设备的资金不超过11000元、监控半径覆盖范围不低于1600米，列出不等式组，根据x的值确定方案，然后对所需资金进行比较，并作出选择．
解：（1）由题意得：
，
解得
；
（2）设购买甲型设备x台，则购买乙型设备（15﹣x）台，依题意得
，
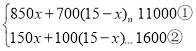解不等式①，得：x≤3
，
解不等式②，得：x≥2，
则2≤x≤3，
∴x取值为2或3．
当x＝2时，购买所需资金为：850×2+700×13＝10800（元），
当x＝3时，购买所需资金为：850×3+700×12＝10950（元），
∴最省钱的购买方案为：购甲型设备2台，乙型设备13台．
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
碟子的个数 | 碟子的高度（单位：cm） |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |
（1）当桌子上放有x（个）碟子时，请写出此时碟子的高度（用含x的式子表示）；
（2）分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
