题目内容
【题目】如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分 ![]() .
.
(1)求过A,B,E三点的抛物线的解析式;
(2)求证:四边形AMCD是菱形;
(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由题意可知,△MBC为等边三角形,点A,B,C,E均在⊙M上,
则MA=MB=MC=ME=2,
又∵CO⊥MB,
∴MO=BO=1,
∴A(﹣3,0),B(1,0),E(﹣1,﹣2),
抛物线顶点E的坐标为(﹣1,﹣2),
设函数解析式为y=a(x+1)2﹣2(a≠0)
把点B(1,0)代入y=a(x+1)2﹣2,
解得:a= ![]() ,
,
故二次函数解析式为:y= ![]() (x+1)2﹣2;
(x+1)2﹣2;
(2)
证明:
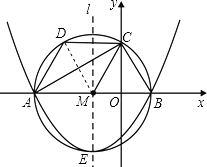
连接DM,
∵△MBC为等边三角形,
∴∠CMB=60°,
∴∠AMC=120°,
∵点D平分弧AC,
∴∠AMD=∠CMD= ![]() ∠AMC=60°,
∠AMC=60°,
∵MD=MC=MA,
∴△MCD,△MDA是等边三角形,
∴DC=CM=MA=AD,
∴四边形AMCD为菱形(四条边都相等的四边形是菱形);
(3)
解:存在.
理由如下:
设点P的坐标为(m,n)
∵S△ABP= ![]() AB|n|,AB=4
AB|n|,AB=4
∴ ![]() ×4×|n|=5,
×4×|n|=5,
即2|n|=5,
解得:n=± ![]() ,
,
当 ![]() 时,
时, ![]() (m+1)2﹣2=
(m+1)2﹣2= ![]() ,
,
解此方程得:m1=2,m2=﹣4
即点P的坐标为(2, ![]() ),(﹣4,
),(﹣4, ![]() ),
),
当n=﹣ ![]() 时,
时, ![]() (m+1)2﹣2=﹣
(m+1)2﹣2=﹣ ![]() ,
,
此方程无解,
故所求点P坐标为(2, ![]() ),(﹣4,
),(﹣4, ![]() ).
).
【解析】此题主要考查了二次函数综合以及菱形的判定方法、三角形面积求法和等边三角形的性质等知识,正确得出E点坐标是解题关键.(1)根据题意首先求出抛物线顶点E的坐标,再利用顶点式求出函数解析式;(2)利用等边三角形的性质结合圆的有关性质得出∠AMD=∠CMD= ![]() ∠AMC=60°,进而得出DC=CM=MA=AD,即可得出答案;(3)首先表示出△ABP的面积进而求出n的值,再代入函数关系式求出P点坐标.
∠AMC=60°,进而得出DC=CM=MA=AD,即可得出答案;(3)首先表示出△ABP的面积进而求出n的值,再代入函数关系式求出P点坐标.

 名校课堂系列答案
名校课堂系列答案【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.