题目内容
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.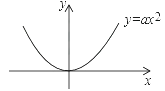
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.
【答案】
(1)解:如图1,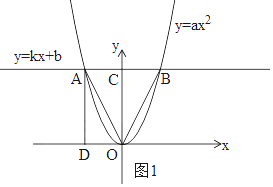
∵抛物线y=ax2的对称轴是y轴,且AB∥x轴,
∴A与B是对称点,O是抛物线的顶点,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,AB⊥OC,
∴AC=BC=1,∠BOC=30°,
∴OC= ![]() ,
,
∴A(-1, ![]() ),
),
把A(-1, ![]() )代入抛物线y=ax2(a>0)中得:a=
)代入抛物线y=ax2(a>0)中得:a= ![]() ;
;
(2)解:如图2,过B作BE⊥x轴于E,过A作AG⊥BE,交BE延长线于点G,交y轴于F,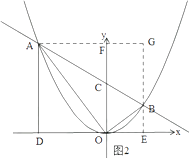
∵CF∥BG,
∴ ![]() ,
,
∵AC=4BC,
∴ ![]() =4,
=4,
∴AF=4FG,
∵A的横坐标为-4,
∴B的横坐标为1,
∴A(-4,16a),B(1,a),
∵∠AOB=90°,
∴∠AOD+∠BOE=90°,
∵∠AOD+∠DAO=90°,
∴∠BOE=∠DAO,
∵∠ADO=∠OEB=90°,
∴△ADO∽△OEB,
∴ ![]() ,
,
∴ ![]() ,
,
∴16a2=4,
a=± ![]() ,
,
∵a>0,
∴a= ![]() ;
;
∴B(1, ![]() );
);
(3)解:如图3,
设AC=nBC,
由(2)同理可知:A的横坐标是B的横坐标的n倍,
则设B(m,am2),则A(-mn,am2n2),
∴AD=am2n2 ,
过B作BF⊥x轴于F,
∴DE∥BF,
∴△BOF∽△EOD,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,DE=am2n,
,DE=am2n,
∴ ![]() ,
,
∵OC∥AE,
∴△BCO∽△BAE,
∴ ![]() ,
,
∴ ![]() ,
,
∴CO= ![]() =am2n,
=am2n,
∴DE=CO.
【解析】(1)抛物线y=ax2关于y轴对称,根据AB∥x轴,得出A与B是对称点,可知AC=BC=1,由∠AOB=60°,可证得△AOB是等边三角形,利用解直角三角形求出OC的长,就可得出点A的坐标,利用待定系数法就可求出a的值。
(2)过B作BE⊥x轴于E,过A作AG⊥BE,交BE延长线于点G,交y轴于F,根据平行线分线段成比例证出AF=4FG,根据点A的横坐标为﹣4,求出点B的横坐标为1,则A(-4,16a),B(1,a),再根据已知证明∠BOE=∠DAO,∠ADO=∠OEB,就可证明△ADO∽△OEB,得出对应边成比例,建立关于a的方程求解,再根据点B在第一象限,确定点B的坐标即可。
(3)根据(2)可知A的横坐标是B的横坐标的n倍,则设B(m,am2),则A(-mn,am2n2),得出AD的长,再证明△BOF∽△EOD,△BCO∽△BAE,得对应边成比例,证得CO=am2n,就可证得DE=CO。

 阅读快车系列答案
阅读快车系列答案【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 | | 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 | | ( |
A.5
B.6
C.7
D.8
【题目】10月21日,“中国流动科技馆”巡展启动仪式在新华区青少年活动中心盛大举行,此次巡展以“体验科学”为主题.该区某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
组别 | 成绩 | 频数 |
A组 |
|
|
B组 |
| 12 |
C组 |
| 18 |
D组 |
| 21 |
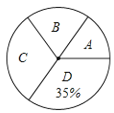
(1)表中一共抽取了________个参赛学生的成绩;![]() ________;
________;
(2)求出计算扇形统计图中“![]() ”的圆心角度数.
”的圆心角度数.
(3)若成绩在90分以上(包括90分)的为“优”等,已知该校共有1200名学生,请你估计该校约有多少名学生的成绩是“优”等.


