Question

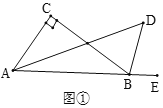
【题目】如图1，矩形ABCD，E为边AB上的点，将△BCE沿CE折叠，点B恰好落在AC上点B′处．

（1）若AB＝8，BC＝6，求BE的长度；

（2）如图2，过点D作EC的垂线，垂足为点G，分别交BC、AC于点F、H，连结EF，若EF＝AE，求证：为定值；

（3）若四边形EFCH是菱形，则＝_____．

Answer 1

【答案】（1）3；（2）证明见解析，；（3）

【解析】

（1）由轴对称的性质可知BE=BE'，∠AB'E=90°，可设BE=BE'=x，通过勾股定理可求出BE的长；

（2）先证∠AEB'=∠ACB，再证∠EFB=∠AEB'=∠ACB并设为，设∠EFD=，可通过平角等于180°列出等量关系式，求出β与α的比值，即可求出结果；

（3）设EF=FC=CH=HE=a，AD=y，证△ADH∽△CFH，求出AD=AH=b，通过△AEH∽△ABC可求出a与b的关系，即可求出最终结论．

解：（1）如图：

∵四边形ABCD为矩形，

∴△ABC为直角三角形，

Rt△ABC中，由勾股定理，

，

由翻折可知：BC=B′C=6，

∴AB′=10－6=4，

设EB=EB′=x，AE=8－x，

Rt△AEB′中，AB′2+EB′2=AE2，

∴42+x2=（8－x）2，

∴x=3，

∴BE=3；

（2）作，如图：

在△AB'E与△ABC中，∠AB'E=∠B=90°，∠EAB'=∠CAB，

∴∠AEB'=∠ACB，

∵BE=B'E，EF=AE，∠AB'E=∠B，

∴Rt△AB'E≌Rt△FBE（HL），

∴∠EFB=∠AEB'，

设∠EFB=∠AEB'=∠ACB=，∠EFD=，

则∠FEG=90°-，

∴∠BEC=+90°-，

由折叠知，∠BEC=∠B'EC，

∵∠BEC+∠B'EC+∠AEB'=90°，

∴2（+90°）+=180°，

∴3=2，

∴，

即为定值；

（3）如图：

设EF=FC=CH=HE=a，AD=y，

∵AD∥BC，

∴△ADH∽△CFH，

∴，

∵CF=CH，

∴AD=AH=b，

∴AC=a+b，

∵EH∥BC，

∴△AEH∽△ABC，

∴，

∴，

∴，

设b=1，则，
∴，

∴，

故答案为：．