题目内容
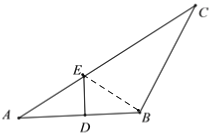
【题目】如图,在等腰△ABC中,AB=BC,∠B=120°,线段AB的垂直平分线分别交AB、AC于点D、E,若AC=12,则DE=___________.

【答案】2
【解析】
先根据等腰三角形性质和三角形内角和定理求出∠A=∠C=30°,根据线段垂直平分线性质和等腰三角形性质求出∠ABE=30°,根据含30度角的直角三角形性质可得CE=BE,继而求出AE长,再根据含30度角的直角三角形性质即可求得答案.
连接BE,
∵在△ABC中,AB=BC,∠ABC=120°,
∴∠A=∠C=30°,
∵AB的垂直平分线DE,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠EBC=120°-30°=90°,
∴CE=2BE,
∵AE+BE=AC=12,
∴AE=4,
又∵∠A=30°,∠ADE=90°,
∴DE=![]() AE=2,
AE=2,
故答案为:2.

练习册系列答案
相关题目





