题目内容
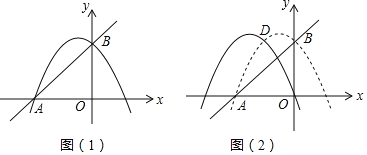
【题目】如图（1），在平面直角坐标系中，抛物线y=
x2+bx+c与x轴交于点A（﹣4，0），与y轴交于点B（0，4）．
（1）求抛物线的函数解析式；
（2）在x轴上有一点P，点P在直线AB的垂线段为PC，C为垂足，且PC=
，求点P的坐标；
（3）如图（2），在（2）的条件下，将原抛物线向左平移，使平移后的抛物线过原点，与原抛物线交于点D，在平移后的抛物线上是否存在点E，使S△APE=S△ACD？若存在，请求出点E的坐标，若不存在，请说明理由．
【答案】（1）
；
（2）点P的坐标为：P1（-2，0），P2（-6，0）
（3）存在点E，E的坐标为：（
，1）或（
，1）或（
， 
）或
（
， 
）
【解析】（1）
（2）点P的坐标为：P1（-2，0），P2（-6，0）
（3）存在点E，E的坐标为：（
，1）或（
，1）或（
， 
）或
（
， 
）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
