题目内容
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点F. 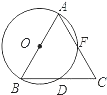
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由.
【答案】
(1)解:连接AD.
∵AB是⊙O的直径,
∴AD⊥BC,
∵BD=CD,
∴AB=AC.
(2)解:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B<∠ADB=90度.
∠C<∠ADB=90度.
∴∠B、∠C为锐角.
∵AC和⊙O交于点F,连接BF,
∴∠A<∠BFC=90度.
∴△ABC为锐角三角形.
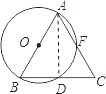
【解析】(1)连接AD,则AD垂直平分BC,那么AB=AC;(2)应把△ABC的各角进行分类,与直角进比较,进而求得△ABC的形状.
【考点精析】认真审题,首先需要了解等腰三角形的判定(如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.

练习册系列答案
相关题目