题目内容
【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

【答案】(1) (2,4)(4,2)答案不唯一;(2)Q点坐标(4,2);(3)最大值是7.5,理由见解析。
【解析】
(1)任取一点A,由图可写出点B坐标,即知点P的关联点Q的坐标,答案不唯一;
(2)先由图确定点P的关联点Q(x,y)的x,y满足的关系式,再联立方程求解;
(3)可将△CAB的面积分割成两部分求解,四边形CAOB及△OAB的面积,四边形CAOB面积为定值,只需求出△OAB的面积的最大值相加即可.
(1)由图可得(2,4)(4,2)答案不唯一
(2)由图可知3-x=y-3,可得x+y=6
联立方程组![]()
解得![]()
∴Q点坐标(4,2)
(3)如图
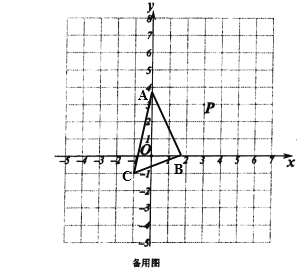
由图可知S△CAB=![]()
![]()
∵x+y=6
![]()
![]()
∵x+y=6
xy最大值是当x=y=3时
所以S△OAB最大值是4.5
所以S△CAB的最大值为![]()

练习册系列答案
相关题目