题目内容
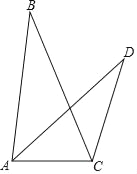
【题目】点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.
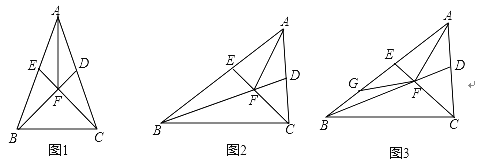
(1)如图1,若∠AEF=∠ADF,求证:AE=AD;
(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;
(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△AEF≌△ADF,根据全等三角形的对应边相等证明结论;
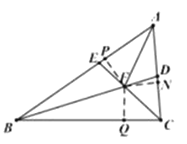
(2)过点F分别作AB,BC,AC边上的高,根据角平分线的性质定理得到FP=FQ,FP=FN,根据角平分线的判定定理得到CF平分∠ACB,证明Rt△PEF≌Rt△NDF,根据全等三角形的性质得到∠PEF=∠FDN,计算得到答案;
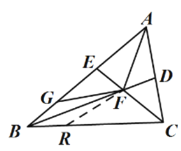
(3)在BC上取点R,使CR=CA,分别证明△CAF≌△CRF、△BGF≌△BRF,根据全等三角形的性质、三角形的周长公式计算即可.
(1)∵![]() ,
,![]() ,
,![]() .
.
∴![]() ,∴
,∴![]() .
.

(2)过![]() 点分别作
点分别作![]() ,
,![]() ,
,![]() 边上的高,
边上的高,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 为垂足.
为垂足.
∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,∴
,∴![]() 平分
平分![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
∴![]() 且
且![]() ,
,
∴![]() .
.
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目