��Ŀ����
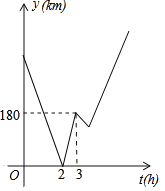
����Ŀ��A��C��B����������һ����ֱ�ĵ�·�ϣ��ס�������ͬʱ�ֱ��A��B���س�����������У��׳���A����ʻ��B�ؾ�ֹͣ���ҳ���B����ʻ��A�غ���������ͬ���ٶȷ���B�أ���������ʻ�Ĺ����У��ס�������������������ʻ���ס���������C�صľ���֮��y��km����׳�������ʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ�����ҳ��ڶ��ε���C��ʱ���׳���B�صľ���Ϊ______km��
���𰸡�120
��������
�ȸ��ݺ���ͼ���ṩ����Ϣ������ҳ����ٶȺͼ׳����ٶȣ���������AB��AC�ij��������ҵڶ��ε���C�ص�ʱ�䣬����׳���B�صľ��룮
������ã�A�ص�C�ؼ�����2��Сʱ��������1��Сʱ��
����ٶ�Ϊakm/h�����ҵ��ٶ�Ϊ2akm/h��
2a+3a-2a=180��
a=60��
��A��B���صľ���Ϊ��2a+4a=6a=360��
A��C���صľ���Ϊ��2��60=120��
�ҵڶ��ε���C�ص�ʱ��Ϊ��![]() =4h��
=4h��
360-4��60=120��ǧ�ף���
�����ҳ��ڶ��ε���C��ʱ���׳���B�صľ���Ϊ120km��
![]()
�ʴ�Ϊ��120��

��ϰ��ϵ�д�
 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
�����Ŀ