Question

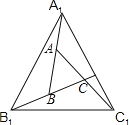
【题目】如图，在正方形ABCD中，点E是AD的中点，连接BE、CE，点F是CE的中点，连接DF、

BF，点M是BF上一点且=，过点M作MN⊥BC于点N，连接FN，则= ．

Answer 1

【答案】

【解析】

试题分析：根据正方形的性质得到∠A=∠ABC=∠BCD=∠CDA=90°，AB=BC=CD=DA，AD∥BC．设AE=a，则DE=a，AB=BC=CD=DA=2a．根据勾股定理得到BE=a，CE=a，得到BE=CE，过点F作FG⊥AD于G，FG交BC于H．根据FG∥CD，点F是CE的中点，得到EG=DG=DE=a，GF=CD=a．根据三角函数的定义得到∠AEB=∠GDF，由平行线的性质得到∠BEF=∠DFE，推出△EFG≌△CFH，根据全等三角形的性质得到FG=FH=a，EG=CH=a．推出四边形CDGH是矩形，根据矩形的性质得到CH=DG=a，根据平行线分线段成比例定理得到==，于是得到MN=FH=a，BN=BH=a，求得S△FMN==a×a=a2，S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣2aa﹣﹣=a2．即可得到结论．

解：∵四边形ABCD是正方形，

∴∠A=∠ABC=∠BCD=∠CDA=90°，AB=BC=CD=DA，AD∥BC．

设AE=a，则DE=a，AB=BC=CD=DA=2a．

在△ABE中，由勾股定理，得BE=a，

在△CDE中，由勾股定理，得CE=a，

∴BE=CE，

过点F作FG⊥AD于G，FG交BC于H．

∵AD∥BC，FG⊥AD，∴GH⊥BC．

∵FG∥CD，点F是CE的中点，

∴EG=DG=DE=a，GF=CD=a．

在直角△ABE中，∵tan∠AEB===2，

在直角△GFD中，∵tan∠GDF===2，

∴tan∠AEB=tan∠GDF，

∵0°＜∠AEB＜90°，0°＜∠GDF＜90°，

∴∠AEB=∠GDF，

∴BE∥DF，

∴∠BEF=∠DFE，

在△EFG与△CFH中，，

∴△EFG≌△CFH，

∴FG=FH=a，EG=CH=a．

∵GH∥CD，GD∥HC，∠CDA=90°，

∴四边形CDGH是矩形，

∴CH=DG=a，

∴BH=BC﹣CH=a．

∵MN⊥BC，GH⊥BC，

∴MN∥FH，

∴==，

∴MN=FH=a，BN=BH=a，

∴MN=AB，

∵BN=CH=a，

∴NH=BC﹣BN﹣CH=a，

∴S△FMN==a×a=a2，

S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣2aa﹣﹣=a2．

∴==．

故答案为：．