题目内容
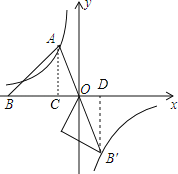
【题目】如图,已知第二象限的点A在反比例函数y=![]() 上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=
上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=![]() 上,则k的值为( )
上,则k的值为( )

A.﹣2![]() B.﹣
B.﹣![]() C.2
C.2![]() D.﹣4
D.﹣4![]()
【答案】D
【解析】
试题分析:作AC⊥x轴于C,B′D⊥x轴于点D,根据反比例函数y=![]() 系数k的几何意义求得S△AOC=
系数k的几何意义求得S△AOC=![]() ×|﹣
×|﹣![]() |=
|=![]() ,进而根据△AOC∽△BOA和直角三角函数求得S△AOB=4×
,进而根据△AOC∽△BOA和直角三角函数求得S△AOB=4×![]() =2
=2![]() ,然后证得△B′OD≌△BOA,得出S△B′OD=S△AOB=2
,然后证得△B′OD≌△BOA,得出S△B′OD=S△AOB=2![]() ,最后根据根据反比例函数y=
,最后根据根据反比例函数y=![]() 系数k的几何意义得出k=﹣4
系数k的几何意义得出k=﹣4![]() .
.
解:作AC⊥x轴于C,B′D⊥x轴于点D,
∵点A在反比例函数y=﹣![]() 上,
上,
∴S△AOC=![]() ×|﹣
×|﹣![]() |=
|=![]() ,
,
∵AB⊥AO,∠AOB=60°,
∴cos∠AOB=![]() =
=![]() ,
,
∵∠ACO=∠BAO=90°,∠AOC=∠BOA,
∴△AOC∽△BOA,
∴![]() =(
=(![]() )2=4,
)2=4,
∴S△AOB=4×![]() =2
=2![]() ,
,
∵将△AOB绕点O逆时针旋转120°,∠AOB=60°,
∴A、O、B′在一条直线上,
∴∠B′OD=∠AOB,OB=OB′,
在△B′OD和△BOA中,
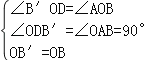 ,
,
∴△B′OD≌△BOA(AAS),
∴S△B′OD=S△AOB=2![]() ,
,
∵S△B′OD=![]() |k|,图象在第四象限,
|k|,图象在第四象限,
∴k=﹣4![]() .
.
故选D.

练习册系列答案
相关题目
