题目内容
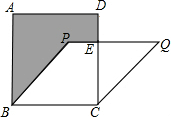已知，如图，正方形ABCD的面积为25，菱形PQCB的面积为20，求阴影部分的面积．
分析：由题意易得AB=BC=BP=PQ=QC=5，EC=4，在Rt△QEC中，可根据勾股定理求得EQ=3，又有PE=PQ-EQ=2，进而可得S阴影的值．
解答：解：∵正方形ABCD的面积是25，
∴AB=BC=BP=PQ=QC=5（1分），
又∵S菱形BPQC=PQ×EC=5×EC=20，
∴S菱形BPQC=BC•EC，
即20=5•EC，
∴EC=4（2分）
在Rt△QEC中，EQ=
=3；
∴PE=PQ-EQ=2，（4分）
∴S阴影=S正方形ABCD-S梯形PBCE=25-
×（5+2）×4=25-14=11．（6分）
∴AB=BC=BP=PQ=QC=5（1分），
又∵S菱形BPQC=PQ×EC=5×EC=20，
∴S菱形BPQC=BC•EC，
即20=5•EC，
∴EC=4（2分）
在Rt△QEC中，EQ=
| QC2-EC2 |
∴PE=PQ-EQ=2，（4分）
∴S阴影=S正方形ABCD-S梯形PBCE=25-
| 1 |
| 2 |
点评：此题主要考查菱形的性质和面积计算以及正方形的性质．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
，连接DF，交BE的延长线于点G，连接OG．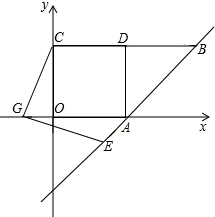
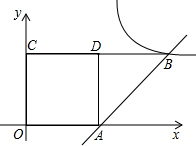
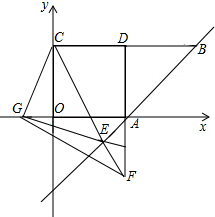
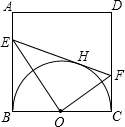于E，交CD于F．
已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．