题目内容
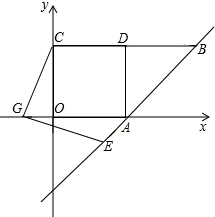
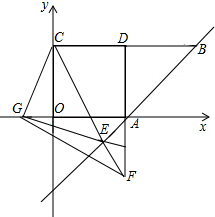
已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE•GB=4-2
| 2 |
分析:(1)根据全等三角形的判定方法寻找条件.
(2)因为O是BD的中点,结合已知条件,知道证明G是DF中点即可.
(3)要求正方形的面积,求出边长的平方即可,为此要找到一个关于边长的方程,因为已知中有直角,根据勾股定理,结合已知条件,列出方程,求出答案.
(2)因为O是BD的中点,结合已知条件,知道证明G是DF中点即可.
(3)要求正方形的面积,求出边长的平方即可,为此要找到一个关于边长的方程,因为已知中有直角,根据勾股定理,结合已知条件,列出方程,求出答案.
解答:(1)证明:在△BCE与△DCF中,
∵
,
∴△BCE≌△DCF.
(2)解:OG=
BF.
理由如下:∵△BCE≌△DCF,
∴∠CEB=∠F,
∵∠CEB=∠DEG,
∴∠F=∠DEG,
∵∠F+∠GDE=90°,
∴∠DEG+∠GDE=90°,
∴BG⊥DF,
∴∠BGD=∠BGF,
又∵BG=BG,∠DBG=∠FBG,
∴△BGD≌△BGF,
∴DG=GF,
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG=
BF.
(3)解:设BC=x,则DC=x,BD=
x,
由(2)知,△BGF≌△BGD,
∴BF=BD,
∴CF=(
-1)x,
∵∠DGB=∠EGD,∠DBG=∠EDG,
∴△GDB∽△GED,
∴
=
,
∴GD2=GE•GB=4-2
,
∵DC2+CF2=(2GD)2,
∴x2+(
-1)2x2=4(4-2
),
(4-2
)x2=4(4-2
),
x2=4,
正方形ABCD的面积是4个平方单位.
∵
|
∴△BCE≌△DCF.
(2)解:OG=
| 1 |
| 2 |
理由如下:∵△BCE≌△DCF,
∴∠CEB=∠F,
∵∠CEB=∠DEG,
∴∠F=∠DEG,
∵∠F+∠GDE=90°,
∴∠DEG+∠GDE=90°,
∴BG⊥DF,
∴∠BGD=∠BGF,
又∵BG=BG,∠DBG=∠FBG,
∴△BGD≌△BGF,
∴DG=GF,
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG=
| 1 |
| 2 |
(3)解:设BC=x,则DC=x,BD=
| 2 |
由(2)知,△BGF≌△BGD,
∴BF=BD,

∴CF=(
| 2 |
∵∠DGB=∠EGD,∠DBG=∠EDG,
∴△GDB∽△GED,
∴
| GD |
| GE |
| GB |
| GD |
∴GD2=GE•GB=4-2
| 2 |
∵DC2+CF2=(2GD)2,
∴x2+(
| 2 |
| 2 |
(4-2
| 2 |
| 2 |
x2=4,
正方形ABCD的面积是4个平方单位.
点评:本题综合考查了全等三角形、正方形、相似三角形的有关知识.注意对全等,相似的综合运用.

练习册系列答案
相关题目



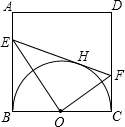 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.