��Ŀ����
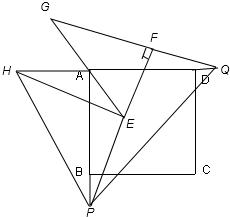
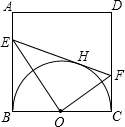
24����֪����ͼ��������ABCD����Rt��EFGб��EG���е����A�غϣ�ֱ�Ƕ���F���������ε�AB���ϣ�Rt��EFG����ֱ�DZ߷ֱ�AB��AD����P��Q���㣬����P���F�غϣ�����ͼ��ʾ��



��1����֤��EP2+GQ2=PQ2��
��2������Rt��EFG���ŵ�A��ʱ����ת����0�㣼����90�㣩����ֱ�DZ߷ֱ�AB��AD����P��Q���㣬��ͼ2��ʾ���ж������߶�EP��PF��FQ��QG֮���Ƿ����ʲôȷ������ȹ�ϵ�������ڣ�֤����Ľ��ۣ��������ڣ���˵�����ɣ�
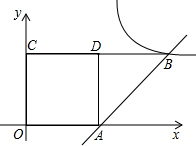
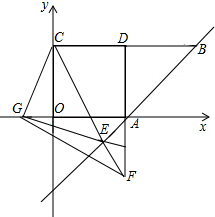
��3������Rt��EFG���ŵ�A��ʱ����ת����90�㣼����180�㣩����ֱ�DZ߷ֱ�AB��AD�����ӳ�����P��Q���㣬���ж������߶�EP��PF��FQ��QG֮����ں���ȷ������ȹ�ϵ������������ͼ3����ֱ��д����Ľ��ۣ�����֤������



��1����֤��EP2+GQ2=PQ2��
��2������Rt��EFG���ŵ�A��ʱ����ת����0�㣼����90�㣩����ֱ�DZ߷ֱ�AB��AD����P��Q���㣬��ͼ2��ʾ���ж������߶�EP��PF��FQ��QG֮���Ƿ����ʲôȷ������ȹ�ϵ�������ڣ�֤����Ľ��ۣ��������ڣ���˵�����ɣ�
��3������Rt��EFG���ŵ�A��ʱ����ת����90�㣼����180�㣩����ֱ�DZ߷ֱ�AB��AD�����ӳ�����P��Q���㣬���ж������߶�EP��PF��FQ��QG֮����ں���ȷ������ȹ�ϵ������������ͼ3����ֱ��д����Ľ��ۣ�����֤������
��������1������E��EH��FG���ɴ˿�֤��EAH�ա�GAQ��Ȼ�����ȫ�������ε����ʵõ�EH=QG����PQ=PH����Rt��EPH�У�EP2+EH2=PH2���ɴ˿��Եõ�EP2+GQ2=PQ2��
��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH���ɴ˿�֤��EAH�ա�GAQ��Ȼ�����ȫ�������ε����ʵõ�EH=QG����PH=PQ����Rt��EPH�У�EP2+EH2=PH2����EP2+GQ2=PH2����Rt��PFQ�У�PF2+FQ2=PQ2����PF2+FQ2=EP2+GQ2��
��3�������߶�EP��PF��FQ��QG֮��Ĺ�ϵΪPE2+GQ2=PF2+FQ2��֤������ͬ�ϣ�
��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH���ɴ˿�֤��EAH�ա�GAQ��Ȼ�����ȫ�������ε����ʵõ�EH=QG����PH=PQ����Rt��EPH�У�EP2+EH2=PH2����EP2+GQ2=PH2����Rt��PFQ�У�PF2+FQ2=PQ2����PF2+FQ2=EP2+GQ2��
��3�������߶�EP��PF��FQ��QG֮��Ĺ�ϵΪPE2+GQ2=PF2+FQ2��֤������ͬ�ϣ�
����⣺ ��1������E��EH��FG����ͼ��ʾ��
��1������E��EH��FG����ͼ��ʾ��
��EA=AG����HEA=��AGO����HAE=��GAD��
���EAH�ա�GAQ��
��EH=QG��HA=AQ��
��FA��AD��
��PQ=PH��
��Rt��EPH��
��EP2+EH2=PH2��
��EP2+GQ2=PQ2��
 ��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH��
��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH��
��EA=AG����HEA=��AGO����HAE=��GAD��
���EAH�ա�GAQ��
��EH=QG��HA=AQ��
��PA��AD��
��PQ=PH��
��Rt��EPH��
��EP2+EH2=PH2��
��EP2+GQ2=PH2��
��Rt��PFQ��
��PF2+FQ2=PQ2��
��PF2+FQ2=EP2+GQ2��
��3�������߶�EP��PF��FQ��QG֮��Ĺ�ϵΪPE2+GQ2=PF2+FQ2��
 ��1������E��EH��FG����ͼ��ʾ��
��1������E��EH��FG����ͼ��ʾ����EA=AG����HEA=��AGO����HAE=��GAD��
���EAH�ա�GAQ��
��EH=QG��HA=AQ��
��FA��AD��
��PQ=PH��
��Rt��EPH��
��EP2+EH2=PH2��
��EP2+GQ2=PQ2��
 ��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH��
��2������E��EH��FG����DA���ӳ����ڵ�H������PQ��PH����EA=AG����HEA=��AGO����HAE=��GAD��
���EAH�ա�GAQ��
��EH=QG��HA=AQ��
��PA��AD��
��PQ=PH��
��Rt��EPH��
��EP2+EH2=PH2��
��EP2+GQ2=PH2��
��Rt��PFQ��
��PF2+FQ2=PQ2��
��PF2+FQ2=EP2+GQ2��
��3�������߶�EP��PF��FQ��QG֮��Ĺ�ϵΪPE2+GQ2=PF2+FQ2��
������������Ҫ��������ת�����ʣ�������ת������������ȫ�������ε��ж�������ͬʱ��������У�Ҫ����ֱ�������κ������ε�����������������⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ������DF����BE���ӳ����ڵ�G������OG��
������DF����BE���ӳ����ڵ�G������OG��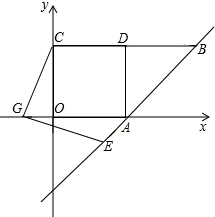
 ��E����CD��F��
��E����CD��F�� ��֪����ͼ��������ֽƬABCD�ı߳���4����M��N�ֱ�������AB��CD�ϣ����е�N�����C�غϣ�����ֱ��MN�۵���ֽƬ����Bǡ������AD���ϵ�E����
��֪����ͼ��������ֽƬABCD�ı߳���4����M��N�ֱ�������AB��CD�ϣ����е�N�����C�غϣ�����ֱ��MN�۵���ֽƬ����Bǡ������AD���ϵ�E����