��Ŀ����
����Ŀ��ij����һ������ʩ���У������γ�����ȵ����е��������ֱ��ס�������ʩ����ͬʱ����ʩ������ͼ�Ƿ�ӳ���������е��ij���y���ף���ʩ��ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺ 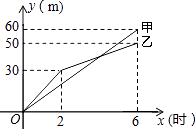
��1�����Ҷ���2��x��6��ʱ����ڣ�y��x�ĺ�����ϵʽ��
��2������ʩ���ٶȲ��䣬�Ҷ���ʩ��6Сʱ��ʩ���ٶ����ӵ�12��/ʱ���������ͬʱ�����������Ӵӿ�ʼʩ������ɣ�����������е����Ƕ����ף�
���𰸡�
��1���⣺�Ҷ���2��x��6��ʱ����ڣ�y��x�ĺ�����ϵʽΪy=kx+b��
![]() ����
���� ![]() ��
��
���Ҷ���2��x��6��ʱ����ڣ�y��x�ĺ�����ϵʽ��y=5x+20
��2���⣺��Ӵӿ�ʼʩ�����������������е���y�ף�
��ͼ��ɵã��ӵ�ʩ���ٶ�Ϊ��60��6=10����/ʱ����
�� ![]() ��
��
��ã�y=110��
���Ӵӿ�ʼʩ�����������������е���110��
����������1�����ݺ���ͼ���е����ݿ�������Ҷ���2��x��6��ʱ����ڣ�y��x�ĺ�����ϵʽ����2����������ͺ���ͼ�������üӵ�ʩ���ٶȣ�Ȼ��������⼴�ɵõ���Ӧ�ķ��̣��Ӷ��������������е����ܵij��ȣ�

��ϰ��ϵ�д�
�����Ŀ