Question

【题目】已知：如图，△ABC的面积为84，BC＝21，现将△ABC沿直线BC向右平移a（0＜a＜21）个单位到△DEF的位置．

（1）求BC边上的高；

（2）若AB＝10，

①求线段DF的长；

②连结AE，当△ABE时等腰三角形时，求a的值．

Answer 1

【答案】（1）8；（2）①DF＝17；②a的值为10或12或．

【解析】

（1）作AM⊥BC于M，根据三角形的面积公式计算；
（2）①根据勾股定理求出BM、AC，根据平移的性质解答；
②分AB=BE、AB=AE、EA=EB三种情况，根据勾股定理计算即可．

（1）作AM⊥BC于M，

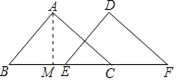
∵△ABC的面积为84，

∴×BC×AM=84，

解得，AM=8，即BC边上的高为8；

（2）①在Rt△ABM中，BM=，

∴CM=BC﹣BM=15，

在Rt△ACM中，AC==17，

由平移的性质可知，DF=AC=17；

②当AB=BE=10时，a=BE=10；

当AB=AE=10时，BE=2BM=12，

则a=BE=12；

当EA=EB=a时，ME=a﹣6，

在Rt△AME中，AM2+ME2=AE2，

即82+（a﹣6）2=a2，

解得，a=，

则当△ABE时等腰三角形时，a的值为10或12或．