题目内容
【题目】如图,AD为△ABC的角平分线,DE⊥AC于E,DF⊥AB于F,EF交AD于点M.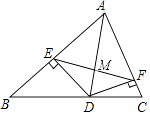
(1)试说明:MF=ME;
(2)若△ABC的面积为28cm2 , AB=20cm,AC=8cm,求DE的长.
【答案】
(1)解:∵AD为△ABC的觉平分线,DE⊥AC,DF⊥AB,
∴DF=DE.
在Rt△AED和Rt△AFD中, ![]() .
.
∴Rt△AED≌Rt△AFD.
∴AE=AF.
∵AE=AF,AD平分∠EAF,
∴EM=MF
(2)解:∵S△ABC=S△ABD+S△ACD,
∴ ![]() ABDF+
ABDF+ ![]() AC×DE=28,即10DF+4DE=28.
AC×DE=28,即10DF+4DE=28.
∵DF=DE,
∴14DE=28,解得DE=2
【解析】(1)依据角平分线的性质可得到ED=DF,然后利用HL可证明Rt△AED≌Rt△AFD,则AE=AF,最后依据等腰三角形三线合一的性质可得到MF=ME;
(2)由S△ABC=S△ABD+S△ACD列方程求解即可.
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③