题目内容
【题目】如图,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°,求∠AOB的度数. 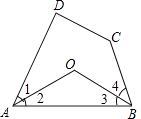
【答案】解:∵∠D+∠C+∠DAB+∠ABC=360°,∠D+∠C=220°,
∴∠DAB+∠ABC=360°﹣220°=140°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=70°,
∴∠AOB=180°﹣70°=110°
【解析】首先根据四边形内角和为360度计算出∠DAB+∠ABC=360°﹣220°=140°,再根据∠1=∠2,∠3=∠4计算出∠2+∠3=70°,然后利用三角形内角和为180度计算出∠AOB的度数.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和多边形内角与外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.

练习册系列答案
相关题目
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③