Question

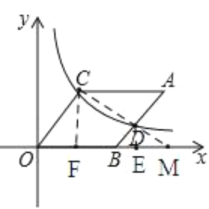
【题目】如图，在平面直角坐标系中，平行四边形ABOC的边OB在x轴上，过点C（3，4）的双曲线与AB交于点D，且AC=2AD，则点D的坐标为_____．

Answer 1

【答案】（7，）．

【解析】

如图，作CF⊥OB于点F，作DE⊥OB于点E，连接CD并延长CD交x轴于点M，根据勾股定理求得OC=5，设AC=2a，则AD=a，OB=2a，DB=5-a，证明△COF∽△DBE，根据相似三角形的性质求得，，即可得D（，），因为点D在反比例函数的图象上，可得方程·=12，解得a=或a=0（舍去）；从而求得点D的坐标.

如图，作CF⊥OB于点F，作DE⊥OB于点E，连接CD并延长CD交x轴于点M，

设反比例函数的解析式为，把点C（3，4）代入求得k=12，即；

∵四边形ABOC是平行四边形，

∴AC∥OB，OC∥AB，AC=OB，AB=OC，

∵C（3，4）

∴OF=3，CF=4，

在Rt△CFO中，根据勾股定理求得OC=5，

∴AB=5.

设AC=2a，则AD=a，OB=2a，

∴DB=5-a，

∵OC∥AB，

∴∠COF=∠DBE，

∵∠CFO=∠BED=90°，

∴△COF∽△DBE，023

∴,

∴，，

∴OE=，

∴D（，），

∵点D在反比例函数的图象上，

∴·=12，

解得a=或a=0（舍去）；

∴D（7， ）.