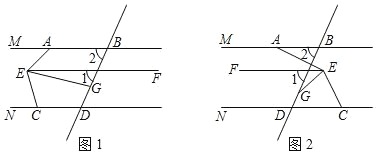题目内容
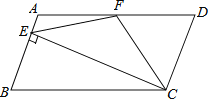
【题目】在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .(1)若点
.(1)若点![]() 恰好落在
恰好落在![]() 边上,则
边上,则![]() ______,(2)延长
______,(2)延长![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,则
,则![]() ______.
______.
【答案】6 ![]() 或
或![]()
【解析】
(1)由矩形的性质得出![]() ,
,![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,由平行线的性质得出
,由平行线的性质得出![]() ,推出
,推出![]() ,得出
,得出![]() ,即可得出结果;
,即可得出结果;
(2)①当点![]() 在矩形
在矩形![]() 内时,连接
内时,连接![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,
,![]() ,
,![]() ,由矩形的性质和
,由矩形的性质和![]() 是
是![]() 的中点,得出
的中点,得出![]() ,
,![]() ,
,![]() ,由
,由![]() 证得
证得![]() ,得出
,得出![]() ,由
,由![]() ,得出
,得出![]() ,
,![]() ,
,![]() ,由勾股定理即可求出
,由勾股定理即可求出![]() ;
;
②当点![]() 在矩形
在矩形![]() 外时,连接
外时,连接![]() ,由折叠的性质得出
,由折叠的性质得出![]() ,
,![]() ,
,![]() ,由矩形的性质和
,由矩形的性质和![]() 是
是![]() 的中点,得出
的中点,得出![]() ,
,![]() ,
,![]() ,由
,由![]() 证得
证得![]() ,得出
,得出![]() ,由
,由![]() ,得出
,得出![]() ,由勾股定理得出:
,由勾股定理得出:![]() ,即
,即![]() ,即可求出
,即可求出![]() .
.
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
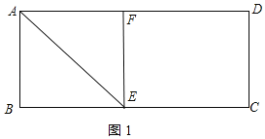
由折叠的性质可知,![]() ,如图1所示:
,如图1所示:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
(2)①当点![]() 在矩形
在矩形![]() 内时,连接
内时,连接![]() ,如图2所示:
,如图2所示:
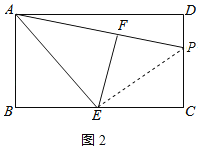
由折叠的性质可知,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
②当点![]() 在矩形
在矩形![]() 外时,连接
外时,连接![]() ,如图3所示:
,如图3所示:
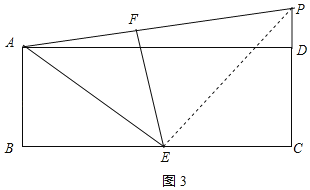
由折叠的性质可知,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即:![]() ,
,
![]() ,
,
解得:![]() ,
,![]() (不合题意舍去),
(不合题意舍去),
综上所述,![]() 或
或![]() ,
,
故答案为:(1)6;(2)![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目