题目内容
【题目】已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD; 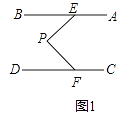
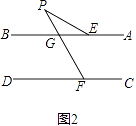
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD; 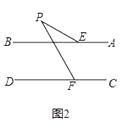
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求 ![]() 的值.
的值. 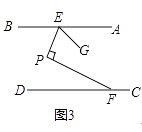
【答案】
(1)解:过P作PQ∥AB,

∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD
(2)证明:∵∠BGP是△PEG的外角,
∴∠P=∠BGP﹣∠BEP.
∵∠P=∠PGB﹣∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD
(3)解:由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°﹣x,
∵∠PEG=∠BEP=90°﹣x,
∴∠AEG=180°﹣2(90°﹣x)=2x,则 ![]() =
= ![]() =2
=2
【解析】(1)过P作PQ平行于AB,由AB与CD平行,得到PQ与CD平行,利用两直线平行内错角相等得到两对角相等,再由∠EPF=∠1+∠2,等量代换就可得证;(2)先根据三角形外角的性质得出∠P=∠BGP﹣∠BEP,再由∠P=∠PGB﹣∠BEP可知,∠PFD=∠PGB,由此可得出结论;(3)由(1)中的结论∠EPF=∠BEP+∠PFD,设设∠PFD=x,则∠BEP=90°﹣x,根据∠PEG=∠BEP=90°﹣x,利用平角定义表示出∠AEG,即可求出所求比值.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目