题目内容
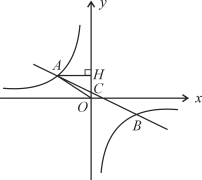
【题目】在平面直角坐标系中，一次函数
（a≠0）的图象与反比例函数
的图象交于第二、第四象限内的A、B两点，与
轴交于点C，过点A作AH⊥轴，垂足为点H，OH=3，tan∠AOH=
，点B的坐标为（
，-2）.
（1）求该反比例函数和一次函数的解析式；
（2）求△AHO的周长.
【答案】（1）一次函数为
，反比例函数为
；（2）△AHO的周长为12
【解析】（1）根据正切函数可得AH=4，根据反比例函数的特点k=xy为定值，列出方程，求出k的值，便可求出反比例函数的解析式；根据k的值求出B两点的坐标，用待定系数法便可求出一次函数的解析式．
（2）由（1）知AH的长，根据勾股定理，可得AO的长，根据三角形的周长，可得答案.
（1）∵tan∠AOH=
=
∴AH=OH=4
∴A（-4，3），代入
，得
k=-4×3=-12
∴反比例函数为
∴
∴m=6
∴B（6，-2）
∴
∴
=
，b=1
∴一次函数为
（2）
△AHO的周长为：3+4+5=12
练习册系列答案
相关题目
