��Ŀ����
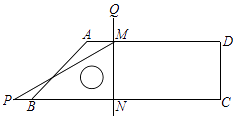
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬ֱ��y=��x��3��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=x2+bx+c����A��C���㣬��x�ύ����һ��B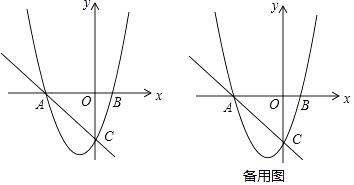
��1���������ߵĽ���ʽ��
��2����D�ǵڶ������������ϵ�һ�����㣬����AD��BD��CD����S��ACD= ![]() S�ı���ACBDʱ����D�����ꣻ
S�ı���ACBDʱ����D�����ꣻ
��3���ڣ�2���������£�����BC������D��DE��BC����CB���ӳ����ڵ�E����P�ǵ��������������ϵ�һ�����㣬��P���ڵ�B�ĶԳƵ�Ϊ��Q������QE���ӳ�QE����������A��D֮��IJ��ֽ���һ��F������DEF+��BPC=��DBEʱ����EF�ij���
���𰸡�
��1��
�⣺����x=0�ã�y=��3��
��C��0����3����
��y=0���x��3=0�����x=��3��
��A����3��0����
��A��C�����������������ߵĽ���ʽ�ģ� ![]() ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪy=x2+2x��3
��2��
�⣺��ͼ1��ʾ��
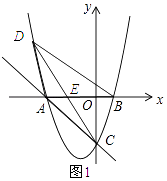
��y=0�ã�x2+2x��3=0�����x=��3��x=1��
��AB=4��
��S��ACD= ![]() S�ı���ACBD��
S�ı���ACBD��
��S��ADC��S��DCB=3��5��
��AE��EB=3��5��
��AE=4�� ![]() =
= ![]() ��
��
���E���������� ![]() ��0����
��0����
��EC�Ľ���ʽΪy=kx+b������C�͵�E���������ã� 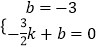 ��
��
��ã�k=��2��b=��3��
��ֱ��CE�Ľ���ʽΪy=��2x��3��
��y=��2x��3��y=x2+2x��3��������ã�x=��4��x=0����ȥ����
��x=��4����y=��2x��3�ã�y=5��
���D����������4��5��
��3��
�⣺��ͼ2��ʾ������D��DN��x�ᣬ����ΪN������P��PM��x�ᣬ����ΪM��
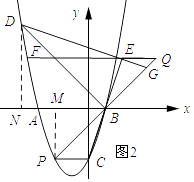
��ֱ��BC�Ľ���ʽΪy=kx+b������C�͵�B���������ã� ![]() ��
��
��ã�k=3��b=��3��
��ֱ��BC�Ľ���ʽΪy=3x��3��
��ֱ��DE�Ľ���ʽΪy=�� ![]() x+n������D���������ã���
x+n������D����������� ![]() ������4��+n=5�����n=5��
������4��+n=5�����n=5�� ![]() =
= ![]() ��
��
��ֱ��DE�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
��y=3x��3��y=�� ![]() x+
x+ ![]() ������ã�x=2��y=3��
������ã�x=2��y=3��
���E������2��3����
���������ľ��빫ʽ��֪��BC=CE= ![]() ��
��
�ߵ�P���Q���ڵ�B�Գƣ�
��PB=BQ��
�ڡ�PCB�͡�QEB�� 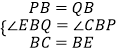 ��
��
���PCB�ա�QEB��
���BPC=��Q��
�֡ߡ�DEF+��BPC=��DBE����DEF=��QEG����EGB=��Q+��QEG
���DBE=��DGB��
�֡ߡ�DBE+��BDE=90�㣬
���DGB+��BDG=90�㣬����PBD=90�㣮
��D����4��5����B��1��0����
��DM=NB��
���DBN=45�㣮
���PBM=45�㣮
��PM=MB
���P��������a��a2+2a��3������BM=1��a��PM=��a2��2a+3��
��1��a=��a2��2a+3����ã�a=��2��a=1����ȥ����
���P����������2��3����
��PC��x�ᣮ
�ߡ�Q=��BPC��
��EQ��PC��
���E���F����������ͬ��
��y=3���������ߵĽ���ʽ�ã�x2+2x��3=3����ã�x=��1�� ![]() ��x=��1+
��x=��1+ ![]() ����ȥ����
����ȥ����
���F����������1 ![]() ��3����
��3����
��EF=2������1�� ![]() ��=3+
��=3+ ![]()
����������1�������A��C��������꣬Ȼ�����ô���ϵ������⼴�ɣ���2�������AB�ij���Ȼ������S��ACD= ![]() S�ı���ACBD �� ���AE�ij����ɵõ�E������Ϊ����
S�ı���ACBD �� ���AE�ij����ɵõ�E������Ϊ���� ![]() ��0�������ô���ϵ���������CE�Ľ���ʽ��Ȼ��CE�Ľ���ʽ�������ߵĽ���ʽ��������õ�D�����ꣻ��3������D��DN��x�ᣬ����ΪN������P��PM��x�ᣬ����ΪM�������BC��DE�Ľ���ʽ���Ӷ�����õ�E�����꣬Ȼ���֤��BC=BE��Ȼ���֤����PCB�ա�QEB���õ���BPC=��Q����������ɵõ���DBE=��DGB������������֤����PBD=90�㣬��DBN=45�㣬Ȼ�����á�PBM=45�㣬���P������Ϊ��a��a2+2a��3������BM=1��a��PM=��a2��2a+3Ȼ������PM=MB�����a��ֵ����ɵõ���P�����꣬Ȼ���֤��EF��x�ᣬ���F����������������ߵĽ���ʽ����õ�F�ĺ����꣬�������EF=xE��xF��⼴�ɣ�
��0�������ô���ϵ���������CE�Ľ���ʽ��Ȼ��CE�Ľ���ʽ�������ߵĽ���ʽ��������õ�D�����ꣻ��3������D��DN��x�ᣬ����ΪN������P��PM��x�ᣬ����ΪM�������BC��DE�Ľ���ʽ���Ӷ�����õ�E�����꣬Ȼ���֤��BC=BE��Ȼ���֤����PCB�ա�QEB���õ���BPC=��Q����������ɵõ���DBE=��DGB������������֤����PBD=90�㣬��DBN=45�㣬Ȼ�����á�PBM=45�㣬���P������Ϊ��a��a2+2a��3������BM=1��a��PM=��a2��2a+3Ȼ������PM=MB�����a��ֵ����ɵõ���P�����꣬Ȼ���֤��EF��x�ᣬ���F����������������ߵĽ���ʽ����õ�F�ĺ����꣬�������EF=xE��xF��⼴�ɣ�

 ��У����ϵ�д�
��У����ϵ�д�