题目内容
【题目】公元3世纪初,我国学家赵爽证明勾定理的图形称为“弦图”.1876年美国总统Garfeild用图1(点C、点B、点C′三点共线)进行了勾股定理的证明.△ACB与△BC′B′是一样的直角三角板,两直角边长为a,b,斜边是c.请用此图1证明勾股定理.
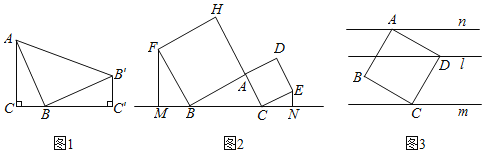
拓展应用l:如图2,以△ABC的边AB和边AC为边长分别向外做正方形ABFH和正方形ACED,过点F、E分别作BC的垂线段FM、EN,则FM、EN、BC的数量关系是怎样?直接写出结论 .
拓展应用2:如图3,在两平行线m、n之间有一正方形ABCD,已知点A和点C分别在直线m、n上,过点D作直线l∥n∥m,已知l、n之间距离为1,l、m之间距离为2.则正方形的面积是 .
【答案】证明勾股定理:见解析;拓展应用l:FM+EN=BC;拓展应用2:正方形的面积为5.
【解析】
用a、b、c表示三角形与梯形的面积,再根据梯形的面积等于三个直角三角形的面积和便可得结论;
拓展1.过点A作AP⊥BC于点P,再证明三角形全等便可得结论;
拓展2.过点D作PQ⊥m,分别交m于点P,交n于点Q,然后证明三角形全等,转化线段,再用勾股定理解答.
如图:
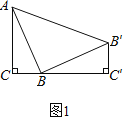
∵点C、点B、点B′三点共线,∠C=∠C′=90°,
∴四边形ACC′B′是直角梯形,
∵△ACB与△BC′B′是一样的直角三角板,
∴Rt△ACB≌Rt△BC′B′,
∴∠CAB=∠C′BB′,AB=BB′,
∴∠CBA+∠C′BB’=90°
∴△ABB′是等腰直角三角形,
所以S梯形ACC′B′=(AC+B′C′)CC′÷2=![]() ,
,
S△ACB=![]() ,S△BC′B′=
,S△BC′B′=![]() ab,S△ABB′=
ab,S△ABB′=![]() c2,
c2,
所以![]() ,
,
a2+2ab+b2=ab+ab+c2,
∴a2+b2=c2;
拓展1.过A作AP⊥BC于点P,如图2,
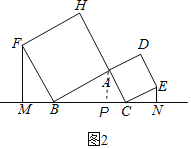
则∠BMF=∠APB=90°,
∵∠ABF=90°,
∴∠BFM+∠MBF=∠MBF+∠ABP,
∴∠BFM=∠ABP,
在△BMF和△ABP中,
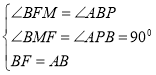 ,
,
∴△BMF≌△ABP(AAS),
∴FM=BP,
同理,EN=CP,
∴FM+EN=BP+CP,
即FM+EN=BC,
故答案为:FM+EN=BC;
拓展2.过点D作PQ⊥m,分别交m于点P,交n于点Q,如图3,
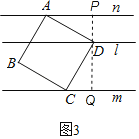
则∠APD=∠ADC=∠CQD=90°,
∴∠ADP+∠DAP=∠ADP+∠CDQ=90°,
∴∠DAP=∠CDQ,
在△APD和△DQC中,
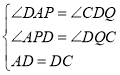 ,
,
∴△APD≌△DQC(AAS),
∴AP=DQ=2,
∵PD=1,
∴
∴正方形的面积为 5,
故答案为:5.





