题目内容
【题目】已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
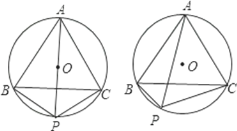
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
【答案】(1)详见解析;(2)结论成立,理由详见解析.
【解析】
(1)连OB,OC,由点P是弧BC的中点,△ABC是⊙O的内接正三角形,根据垂径定理的推论得到AP为⊙O的直径,易得△OBP和△OPC都是等边三角形,于是得到结论;
(2)截取PE=PC,则△PEC为等边三角形,得到CE=CP,∠PCE=60°,易证△CAE≌△CBP,得到AE=PB,即有PB+PC=PA.
(1)连OB,OC,如图
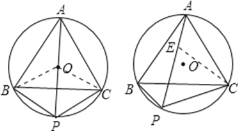
∵点P是弧BC的中点,△ABC是⊙O的内接正三角形,
∴AP为⊙O的直径,
∴∠BPO=∠ACB,∠APC=∠ABC,
∵△ABC是⊙O的内接正三角形,
∴∠ACB=∠ABC=60°,
∴∠BPO=∠APC=60°,
∴△OBP和△OPC都是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA;
(2)(1)的结论还成立.理由如下:
截取PE=PC,
∵∠APC=60°,
∴△PEC为等边三角形,
∴CE=CP,∠PCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCP,
而CA=CB,
∴△CAE≌△CBP,
∴AE=PB,
∴PB+PC=PA.

练习册系列答案
相关题目