题目内容
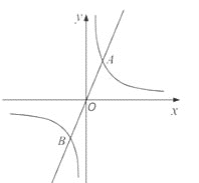
【题目】如图,直线y=3x与反比例函数y=![]() (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.

(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=![]() (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.
①当t=![]() 时,求线段EF的长;
时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.
【答案】(1)m=3;k=3;B(-1,-3);(2)①EF=8,②-1<t≤-![]() 或
或 ![]() ≤t<1
≤t<1
【解析】
(1)把A的坐标代入正比例函数即可得出m的值,把A的坐标代入反比例函数的解析式即可得到k的值,根据对称性即可得到B的坐标;
(2)①把t的值分别代入正比例函数和反比例函数,即可得出结论;
②根据图象即可得出结论.
(1)解:∵直线y=3x与反比例函数y=![]() (k≠0的常数)的图象交于A(1,m),∴m=3,k=3.根据对称性可得:B(-1,-3).
(k≠0的常数)的图象交于A(1,m),∴m=3,k=3.根据对称性可得:B(-1,-3).
(2)解:①当t=![]() 时,y=3x=1,y=
时,y=3x=1,y=![]() =9,∴EF=9-1=8;
=9,∴EF=9-1=8;
②由图象知:-1<t≤-![]() 或
或 ![]() ≤t<1.
≤t<1.

练习册系列答案
相关题目