题目内容
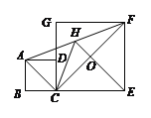
【题目】如图,点E,F分别在正方形ABCD的边CD,BC上,且![]() ,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转
,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转![]() 得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.
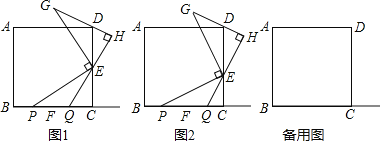
(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为________.
(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形ABCD的边长为6,![]() ,
,![]() ,请直接写出线段BP的长.
,请直接写出线段BP的长.
【答案】(1)![]() ;(2)成立,见解析;(3)线段BP的长为3或5.
;(2)成立,见解析;(3)线段BP的长为3或5.
【解析】
(1)由ASA证明![]() ,得出
,得出![]() ,即可得出结论;
,即可得出结论;
(2)由ASA证明![]() ,得出
,得出![]() ,即可得出结论;
,即可得出结论;
(3)①当点P在线段BF上时,点Q在线段BC上,由(2)可知:![]() ,求出
,求出![]() ,
,![]() ,即可得出答案;
,即可得出答案;
②当点P在射线FC上时,点Q在线段BC的延长线上,同理可得:![]() ;即可得出答案.
;即可得出答案.
(1)![]() ;理由如下:
;理由如下:
∵四边形ABCD是正方形,
∴![]() ,
,![]() ,
,
由旋转的性质得:![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,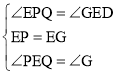 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
故答案为:![]() ;
;
(2)(1)中的结论仍然成立,理由如下:
由题意得:![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵四边形ABCD是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,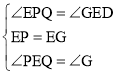 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)分两种情况:
①当点P在线段BF上时,点Q在线段BC上,
由(2)可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
②当点P在射线FC上时,点Q在线段BC的延长线上,如图3所示:
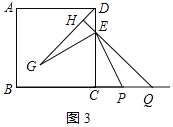
同(2)可得:![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
综上所述,线段BP的长为3或5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目