题目内容
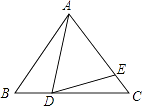
【题目】如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D。
（1）求证：BC是⊙O切线；
（2）若BD=5， DC=3，求AC的长。
【答案】
（1）证明: 如图1，连接OD.
∵ OA=OD, AD平分∠BAC，
∴ ∠ODA=∠OAD, ∠OAD=∠CAD，
∴ ∠ODA=∠CAD，
∴ OD//AC，
∴ ∠ODB=∠C=90°，
∴ BC是⊙O的切线；
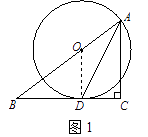
（2）解：如图2，过D作DE⊥AB于E.
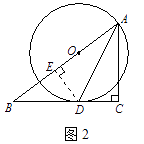
∴ ∠AED=∠C=90°，
又∵ AD=AD, ∠EAD=∠CAD,
∴ △AED≌△ACD.
∴ AE=AC, DE=DC=3，在Rt△BED中，∠BED =90°,由勾股定理，得BE= 
.设AC=x（x>0）, 则AE=x，在Rt△ABC中，∠C=90°, BC=BD+DC=8, AB=x+4, 由勾股定理，得 
，
解得x=6，即 AC=6.
【解析】（1）要证BC是⊙O切线，点D在圆上，因此连接OD，需证明OD⊥BC。先根据等腰三角形的性质及角平分线的定义，证明∠ODA=∠CAD，再根据平行线的判定及性质证明∠ODB=∠C=90°，即可得出结论。
（2）抓住已知AD是∠BAC的平分线，DC⊥AC，根据角平分线的性质添加辅助线过D作DE⊥AB于E，得出DE=DC=3，根据勾股定理求出BE的长，再证明△AED≌△ACD，得出AE=AC，然后在Rt△ABC中，根据勾股定理即可求出AC的长。
【考点精析】通过灵活运用平行线的判定与性质和角平分线的性质定理，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上即可以解答此题．
