��Ŀ����
��֪����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A������Ϊ��0��2������OAΪֱ����ԲB������D��x���ϵ�һ���㣬����AD��ԲB�ڵ�C����1����tan��DAO=
| 1 | 2 |
��2������D��DP��y�����B��C�����ֱ�߽��ڵ�P������������������������ĵ�P�����꣬��ȷ��ͼ����������Ķ��κ����Ľ���ʽ��
��3������P���㣨2���е���������M������Ϊ��-3��3�������߶�PM��PB�ĺ͵���Сֵ���������ʱ��P�����꣮
��������1��ֱ����OA��Բ��ΪB����B��0��1��������tan��1=tan��2=
���ֱ��ֱ�ǡ�OKC����AKC�ɵ�C������Ϊ��
��
������A��0��2���������ֱ��BC����ʽ��
��2������𰸲�Ψһ����ѡ����D�����꣬�Ƴ���P�����꣬���ѡ�����y��ĶԳƵ㣬ʹ�����߽���ʽ��һЩ��
��3������BC=BA��PD��y�ᣬ��PC=PD�����������ת����PM+PB=PM+PC+CB=PM+PD+CB����ֻ�е�ֱ��DP������M��-3��3��ʱ��PM+PD��ֵ��С�����и��߶�����CD����ƽ�е����������Σ��������Ʊ���PD��ȷ��P�����꣮
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
��2������𰸲�Ψһ����ѡ����D�����꣬�Ƴ���P�����꣬���ѡ�����y��ĶԳƵ㣬ʹ�����߽���ʽ��һЩ��
��3������BC=BA��PD��y�ᣬ��PC=PD�����������ת����PM+PB=PM+PC+CB=PM+PD+CB����ֻ�е�ֱ��DP������M��-3��3��ʱ��PM+PD��ֵ��С�����и��߶�����CD����ƽ�е����������Σ��������Ʊ���PD��ȷ��P�����꣮
���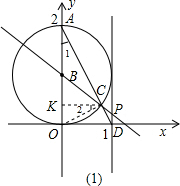 �⣺��1����ͼ��ʾ������D��x�����������ʱ������OC����C����CK��y���ڵ�K��
�⣺��1����ͼ��ʾ������D��x�����������ʱ������OC����C����CK��y���ڵ�K��
��OAΪԲB��ֱ������C��ԲB��
���ACO=90��
���1=��2
��tan��1=
��tan��2=
��OK�ij�Ϊx����KC=2x���ɵ�AK=4x
�ߵ�A������Ϊ��0��2����OK+KA=OA
���B��������0��1����5x=2
��x=
��KC=
���C��������
��
��
��ֱ��BC�Ľ���ʽΪy=kx+1��k��1����
�ã�
=
k+1
��k=-
��ֱ��BC�Ľ���ʽΪy=-
x+1
����D��x��ĸ�������ʱ��ͬ���ɵ�ֱ��BC�Ľ���ʽΪy=
x+1
�����������ֱ��BC�Ľ���ʽΪy=-
x+1��y=
x+1��
��2����DP��y��
��DP��x��
����Dλ����ͼ��λ��ʱ����D��1��0��
�ɵ�P���������Ϊy=-
��1+1=
���P��������1��
��
��ͼ��ʾ������D������Ϊ��2��0��ʱ����AODΪ����������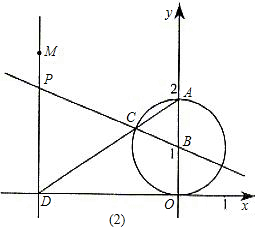
����OC
��OAΪԲB��ֱ��
��OC��AD
��CΪAD�е�
��BC��OD
�֡�DP1��y��
���P1��������2��1��
��ͼ��ʾ�����Ƶأ��ɵõ�P2������Ϊ��-2��1��
��ͼ��P��P1��P2������Ķ��κ����Ľ���ʽΪy=ax2+bx+c��a��0�����ã�
��
=a+b+c����1=4a+2b+c����1=4a-2b+c
���a=
��b=0��c=0
��ͼ��������Ķ��κ����Ľ���ʽΪy=
x2��
��3����ͼ��ʾ
��AB��PD��
��PD��x�ᣬ
=
��AB=BC
��DP=PC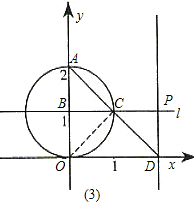
��PM+PB=PM+PC+BC
=PM+PD+BC
�ɼ���֪ʶ��֪����ֱ��DP������M��-3��3��ʱ��PM+PD��ֵ��С
�֡�BC��ԲB�İ뾶
�൱ֱ��BP����Mʱ��PM+PB��ֵ��С
��PM+PB����Сֵ��MD+BC=3+1=4
��OD=3��OA=2
�ɹ��ɶ�����AD=
�ֿ�֤DO��ԲB������
��OD2=DC•AD
��CD=
��
��AC=AD-CD=
�ɡ�PDC�ס�BAC���ã�
=
��DP=
=
���P��������-3��
����
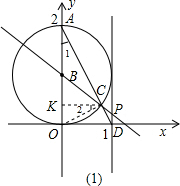 �⣺��1����ͼ��ʾ������D��x�����������ʱ������OC����C����CK��y���ڵ�K��
�⣺��1����ͼ��ʾ������D��x�����������ʱ������OC����C����CK��y���ڵ�K����OAΪԲB��ֱ������C��ԲB��
���ACO=90��
���1=��2
��tan��1=
| 1 |
| 2 |
��tan��2=
| 1 |
| 2 |
��OK�ij�Ϊx����KC=2x���ɵ�AK=4x
�ߵ�A������Ϊ��0��2����OK+KA=OA
���B��������0��1����5x=2
��x=
| 2 |
| 5 |
��KC=
| 4 |
| 5 |
���C��������
| 4 |
| 5 |
| 2 |
| 5 |
��ֱ��BC�Ľ���ʽΪy=kx+1��k��1����
�ã�
| 2 |
| 5 |
| 4 |
| 5 |
��k=-
| 3 |
| 4 |
��ֱ��BC�Ľ���ʽΪy=-
| 3 |
| 4 |
����D��x��ĸ�������ʱ��ͬ���ɵ�ֱ��BC�Ľ���ʽΪy=
| 3 |
| 4 |
�����������ֱ��BC�Ľ���ʽΪy=-
| 3 |
| 4 |
| 3 |
| 4 |
��2����DP��y��
��DP��x��
����Dλ����ͼ��λ��ʱ����D��1��0��
�ɵ�P���������Ϊy=-
| 3 |
| 4 |
| 1 |
| 4 |
���P��������1��
| 1 |
| 4 |
��ͼ��ʾ������D������Ϊ��2��0��ʱ����AODΪ����������

����OC
��OAΪԲB��ֱ��
��OC��AD
��CΪAD�е�
��BC��OD
�֡�DP1��y��
���P1��������2��1��
��ͼ��ʾ�����Ƶأ��ɵõ�P2������Ϊ��-2��1��
��ͼ��P��P1��P2������Ķ��κ����Ľ���ʽΪy=ax2+bx+c��a��0�����ã�
��
| 1 |
| 4 |
���a=
| 1 |
| 4 |
��ͼ��������Ķ��κ����Ľ���ʽΪy=
| 1 |
| 4 |
��3����ͼ��ʾ
��AB��PD��
��PD��x�ᣬ
| AB |
| DP |
| BC |
| PC |
��AB=BC
��DP=PC

��PM+PB=PM+PC+BC
=PM+PD+BC
�ɼ���֪ʶ��֪����ֱ��DP������M��-3��3��ʱ��PM+PD��ֵ��С
�֡�BC��ԲB�İ뾶
�൱ֱ��BP����Mʱ��PM+PB��ֵ��С
��PM+PB����Сֵ��MD+BC=3+1=4
��OD=3��OA=2
�ɹ��ɶ�����AD=
| 13 |
�ֿ�֤DO��ԲB������
��OD2=DC•AD
��CD=
| 9 | ||
|
��AC=AD-CD=
| 4 | ||
|
�ɡ�PDC�ס�BAC���ã�
| PD |
| AB |
| DC |
| AC |
��DP=
| AB•DC |
| AC |
| 9 |
| 4 |
���P��������-3��
| 9 |
| 4 |
�����������ۺ���ǿ��������ֱ����Բ����������Բ�����֪ʶ����������ϵĹ۵㣬ֻ�е�D��P��M���㹲��ʱPM+PD��ֵ��С������и��߶��������Ʊ����P�����꣮

��ϰ��ϵ�д�
�����Ŀ

 ��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��
��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ�� ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������