题目内容
【题目】如图,已知∠AOB=∠COD=90°.
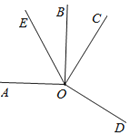
(1)猜想:∠BOC与∠AOD之间的数量关系,并说明理由;
(2)若OE平分∠AOC,∠BOC=34°,求∠AOE的余角的度数;
(3)若OC表示北偏东34°方向,在(2)的条件下直接写出OE表示的方向.
【答案】(1)∠BOC+∠AOD=180°,理由见解析;(2)28°;(3)OE表示的方向为北偏西28°
【解析】
(1)首先根据图形可知∠AOB+∠BOC+∠COD+∠AOD=360°,据此进一步用它们四个角的和减去∠AOB与∠COD即可得出答案;
(2)首先根据题意求出∠AOC的度数,然后利用角平分线性质得出∠AOE的度数,最后进一步计算出它的余角即可;
(3)根据题意可求出∠BOE度数,然后参照OC表示北偏东34°方向即可得出OE表示的方向.
(1)∠BOC与∠AOD之间的数量关系为:∠BOC+∠AOD=180°,
理由如下:
∵∠AOB=∠COD=90°,∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠BOC+∠AOD=360°∠AOB∠COD=180°;
(2)∵∠AOB=90°,∠BOC=34°,
∴∠AOC=∠AOB+∠BOC=124°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=62°,
∠AOC=62°,
∴90°62°=28°,
即∠AOE的余角为28°;
(3)由(2)可得:∠AOE =62°,
∵∠AOB =90°,
∴∠BOE=90°62=28°,
∵OC表示北偏东34°方向,
∴OE表示的方向为北偏西28°.

练习册系列答案
相关题目