题目内容
 如图,已知:正△OAB的面积为4
如图,已知:正△OAB的面积为4| 3 |
| k |
| x |
| k |
| x |
(1)求点B的坐标及k的值;
(2)求m=1和m=3时,S的值.
分析:(1)B点的坐标可通过分别向x轴,y轴作垂线得到,然后根据等边三角形的性质可知横坐标是
OA,纵坐标是三角形的高的长度.
(2)找到m=1和m=3时P的位置,用总面积-2×重叠部分的面积=不重叠部分的面积,根据次等连关系可求解.
| 1 |
| 2 |
(2)找到m=1和m=3时P的位置,用总面积-2×重叠部分的面积=不重叠部分的面积,根据次等连关系可求解.
解答: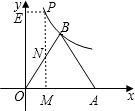 解:(1)设
解:(1)设
OA=x,则三角形的高为
x,
∵正△OAB的面积为4
.
∴
2x•
x=4
x=2.
故B点的坐标是(2,2
).
k=xy=2×2
=4
;
(2)∵m=1,y=
,
∴n=4
.
∵OM=1,
∴MN=
.
∴S=1×4
+4
-
×1×
×2=7
∵m=3,y=
,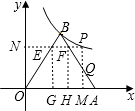
∴n=
;
∴EG=
,
∴OG=
,
∴EF=4-
×2=
.
∴梯形EFAO的面积是:
(
+4)×
=
.
△QMA的面积为:
×
×1=
.
∴S=3×
+4
-2×
+2×
=
.
 解:(1)设
解:(1)设| 1 |
| 2 |
| 3 |
∵正△OAB的面积为4
| 3 |
∴
| 1 |
| 2 |
| 3 |
| 3 |
x=2.
故B点的坐标是(2,2
| 3 |
k=xy=2×2
| 3 |
| 3 |
(2)∵m=1,y=
4
| ||
| x |
∴n=4
| 3 |
∵OM=1,
∴MN=
| 3 |
∴S=1×4
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∵m=3,y=
4
| ||
| x |

∴n=
4
| ||
| 3 |
∴EG=
4
| ||
| 3 |
∴OG=
| 4 |
| 3 |
∴EF=4-
| 4 |
| 3 |
| 4 |
| 3 |
∴梯形EFAO的面积是:
| 1 |
| 2 |
| 4 |
| 3 |
4
| ||
| 3 |
32
| ||
| 9 |
△QMA的面积为:
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴S=3×
4
| ||
| 3 |
| 3 |
32
| ||
| 9 |
| ||
| 2 |
17
| ||
| 9 |
点评:本题考查反比例函数的综合运用,关键能通过点确定函数式,由函数式确定点,本题求不重叠部分的面积关键是把重叠部分求出来,问题可解.

练习册系列答案
相关题目
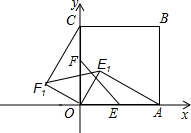 2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.
2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.
 如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=
如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=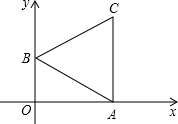 如图,已知等边△ABC的边长为2,顶点A、B分别在x轴、y轴的正半轴上移动.
如图,已知等边△ABC的边长为2,顶点A、B分别在x轴、y轴的正半轴上移动. 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=
如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=