题目内容
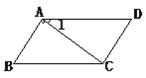
【题目】如图所示，在等边三角形ABC中，BC边上的高AD＝10，E是AD上一点，现有一动点P沿着折线A－E－C运动，在AE上的速度是4单位/秒，在CE上的速度是2单位/秒，则点P从A到C的运动过程中至少需_______秒．
【答案】5
【解析】
如图，作CH⊥AB于H交AD于E．P沿着折线A-E-C运动的时间=
+
=
(EC+AE)= (EC+EH)= CH，根据垂线段最短可知，当CH⊥AB时，P沿着折线A-E-C运动的时间最短，由此即可解决问题．
如图，作CH⊥AB于H交AD于E.
∵△ABC是等边三角形，AD⊥BC，
∴∠HAE=30°,∵∠AHE=90°，
∴HE=AE，
∵P沿着折线AEC运动的时间=+= (EC+AE)= (EC+EH)= CH，
根据垂线段最短可知，当CH⊥AB时，P沿着折线AEC运动的时间最短，
∵CH、AD是等边三角形的高，
∴CH=AD=10，
∴P沿着折线AEC运动的时间最时间=5s.
故答案为5.
练习册系列答案
小夫子全能检测系列答案
相关题目
【题目】某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：
A种产品 | B种产品 | |
成本（万元/件） | 2 | 5 |
利润（万元/件） | 1 | 3 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
