题目内容
【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
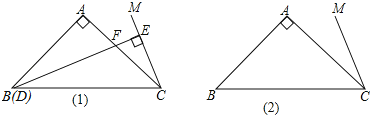
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
【答案】(1)见解析;(2)DF=2CE
【解析】
试题分析:(1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.
解:(1)如图(1),延长BA,CM交点N,
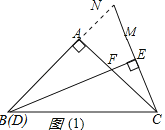
∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中,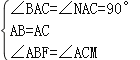 ,
,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE;
(2)保持上述关系;BF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,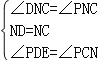 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案