Question

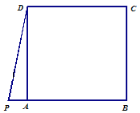
【题目】已知在梯形ABCD中，AD∥BC，AB=BC，DC⊥BC，且AD=1，DC=3，点P为边AB上一动点，以P为圆心，BP为半径的圆交边BC于点Q．

(1)求AB的长；

(2)当BQ的长为时，请通过计算说明圆P与直线DC的位置关系．

Answer 1

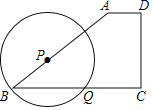
【答案】（1）AB长为5;（2）圆P与直线DC相切，理由详见解析.

【解析】

（1）过A作AE⊥BC于E，根据矩形的性质得到CE=AD=1，AE=CD=3，根据勾股定理即可得到结论；
（2）过P作PF⊥BQ于F，根据相似三角形的性质得到PB=，得到PA=AB-PB=，过P作PG⊥CD于G交AE于M，根据相似三角形的性质得到PM=，根据切线的判定定理即可得到结论．

（1）过A作AE⊥BC于E，
则四边形AECD是矩形，
∴CE=AD=1，AE=CD=3，
∵AB=BC，
∴BE=AB-1，
在Rt△ABE中，∵AB2=AE2+BE2，
∴AB2=32+（AB-1）2，
解得：AB=5；
（2）过P作PF⊥BQ于F，
∴BF=BQ=，
∴△PBF∽△ABE，
∴，
∴，
∴PB=，
∴PA=AB-PB=，
过P作PG⊥CD于G交AE于M，
∴GM=AD=1，

∵DC⊥BC

∴PG∥BC
∴△APM∽△ABE，
∴，
∴，
∴PM=，
∴PG=PM+MG==PB，
∴圆P与直线DC相切．