题目内容
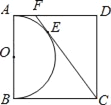
【题目】如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则sin∠FCD=( )
A. ![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由四边形ABCD为正方形,得到四个内角为直角,四条边相等,可得出AD与BC都与半圆相切,利用切线长定理得到FA=FE,CB=CE,设正方形的边长为4a,FA=FE=x,由FE+FC表示出EC,由AD﹣AF表示出FD,在直角三角形FDC中,利用勾股定理列出关系式,用a表示出x,进而用a表示出FD与FC,利用锐角三角函数定义即可求出sin∠FCD的值.
解:∵四边形ABCD为正方形,
∴∠A=∠B=90°,AB=BC=CD=AD,
∴AD与BC都与半圆O相切,又CF与半圆相切,
∴AF=EF,CB=CE,
设AB=BC=CD=AD=4a,AF=EF=x,
∴FC=EF+EC=4a+x,FD=AD﹣AF=4a﹣x,
在Rt△DFC中,由勾股定理得:FC2=FD2+CD2,
∴(4a+x)2=(4a﹣x)2+(4a)2,
整理得:x=a,
∴FC=4a+x=5a,FD=4a﹣x=3a,
∴在Rt△DFC中,sin∠FCD=![]() .
.
故选:B.

练习册系列答案
相关题目