Question

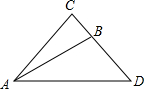
如图，已知B，C，D，E四点在同一条直线上，且BA=BD，CA=CE
（1）当∠BAC=100°，∠ACB=50°时，∠1=______
（2）当∠BAC=100°，∠ACB=70°时，∠1=______
（3）当∠BAC=80°，∠ACB=50°时，∠1=______
（4）当∠BAC=80°，∠ACB=70°时，∠1=______
由上述可知，∠1的大小与∠ACB的大小无关，只与∠BAC的大小有关，猜想∠1与∠BAC有怎样的等量关系？并说明理由．

Answer 1

（1）∵∠BAC=100°，∠ACB=50°，
∴∠B=30°，
又∵BA=BD，∴∠BAD═∠ADB=

1

2

（180°-∠B）=75°，
∵∠ACB=50°，CA=CE，
∴∠AEC=∠CAE=

1

2

（180°-∠C）=65°，
∴在△EAD中，∠BAE=180°-75°-65°=40°，
故答案为：40°；

（2）同（1）可得∠1=40°；

（3）同（1）可得∠1=50°；

（4）同（1）可得∠1=50°．

猜想：∠1+

1

2

∠BAC=90°．
理由：∵BA=BD，
∴∠ADE=

1

2

（180°-∠B）=90°-

1

2

∠B，
∵CA=CE，
∴∠AEC=

1

2

（180°-∠ACB）=90°-

1

2

∠C，
∴在△EAD中，
∠BAE=180°-∠AEC-∠ADB
=180°-（90°-

1

2

∠B）-（90°-

1

2

∠C）

=

1

2

∠B+

1

2

∠C
=

1

2

（180°-∠BAC）
=90°-

1

2

∠BAC，
∴∠1+

1

2

∠BAC=90°．