题目内容
【题目】综合与实践：
问题情境：在一次综合实践活动课上，同学们以菱形为对象，研究菱形旋转中的问题：
已知，在菱形ABCD中，BD为对角线，
，AB=4，将菱形ABCD绕顶点A顺时针旋转，旋转角为
（单位°）．旋转后的菱形为
．在旋转探究活动中提出下列问题，请你帮他们解决．
观察证明：
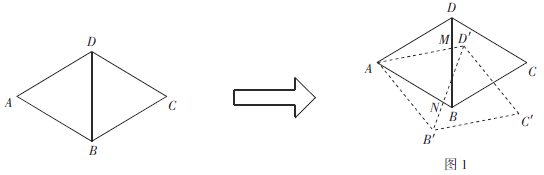
（1）如图1，若旋转角
，
与BD相交于点M，AB与
相交于点N．请说明线段DM与
的数量关系；
操作计算：
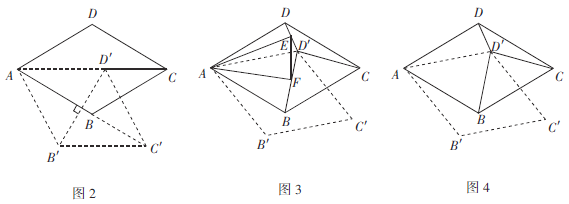
（2）如图2，连接
，菱形ABCD旋转的过程中，当与AB互相垂直时，的长为 ；
（3）如图3，若旋转角，分别连接
，
，过点A分别作
，
，连接EF，菱形ABCD旋转的过程中，发现在
中存在长度不变的线段EF，请求出EF长度；
操作探究：
（4）如图4，在（3）的条件下，请判断以，，三条线段长度为边的三角形是什么特殊三角形，并说明理由．
【答案】（1）
，理由见解析；（2）
；（3）2；（4）以
，
，
三条线段为边的三角形是直角三角形，理由见解析
【解析】
（1）根据旋转的性质利用ASA易证得
，从而证得
；
（2）证得点
在菱形的对角线AC上，即可求解；
（3）利用等腰三角形三线合一的性质证明EF是
的中位线，即可求解；
（4）以
为边向外作等边三角形
，利用
证得
，求得
，即可求解．
（1），
理由如下：
∵四边形ABCD是菱形，
∴AB= AD．
∴∠ADB=∠ABD，
由旋转的性质可得：
，
∴
，
∴
，
∴
，
在
和
中，
，
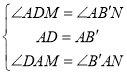∴(ASA) ，
∴；
（2）连接菱形ABCD的对角线AC、BD相交于O，
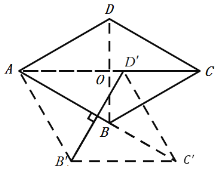
∵四边形ABCD是菱形，且
，AB=4，
∴
，
∴
，则
，
根据旋转的性质，且
与AB互相垂直，
∴
，
∴点在菱形ABCD的对角线AC上，
∴
∴
；
（3）如图，连接BD，
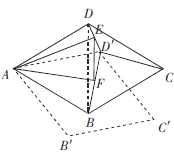
根据旋转的性质可知：
∵ AE⊥D，
∴
（等腰三角形三线合一），同理BF=F，
∴EF是的中位线，
∴
，
∵四边形ABCD是菱形，
∴AB=AD，
又∵
，
是等边三角形，
∴
，
∴
；
（4）以，
，
三条线段为边的三角形是直角三角形，
理由如下：
如图，以为边向外作等边三角形，连接DB，CM,
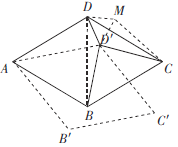
∵四边形ABCD是菱形，，
∴
与
是等边三角形，
，
由（3）可知：
与
都是等腰三角形，
∴
，
∵与
都是等边三角形，
∴
，
，
，
∴
，
∴
，
在
和中，
，
∴
，
∴
，
,
∴
，
∴
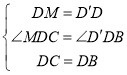是直角三角形，
即以
，，三条线段长度为边的三角形是直角三角形．
