Question

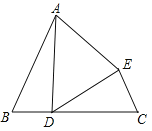
【题目】我们知道，图形的运动只改变图形的位置，不改变图形的形状、大小，运动前后的两个图形全等，翻折就是这样．如图1，将△ABC沿AD翻折，使点C落在AB边上的点C'处，则△ADC≌△ADC'．

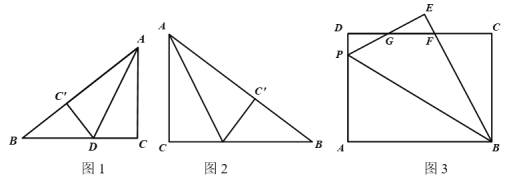
尝试解决：（1）如图2，△ABC中，∠C=90°，AC=6，BC=8，将△ABC沿AD翻折，使点C落在AB边上的点C'处，求CD的长．

（2）如图3，在长方形ABCD中，AB=8，AD=6，点P在边AD上，连接BP，将△ABP沿BP翻折，使点A落在点E处，PE、BE分别与CD交于点G、F，且DG=EG．

①求证：PE=DF；

②求AP的长．

Answer 1

【答案】（1）5；（2）①见解析；②

【解析】

（1）利用勾股定理求出AB，由翻折及三角形全等的性质得到，，再利用勾股定理求出CD；

（2）①由翻折可知△PAB≌△PEB，根据ASA证明△DPG≌△EFG，即可求出结论；

②先将BF、CF分别用PA表示出来，再根据勾股定理求出PA即可.

解：（1）在△ABC中，∠C=90°，AC=6，BC=8，

∴AB=10，

由翻折可知，

∴，，

∴

∵，

∴

∴是直角三角形，且，

∴

∴，

∴CD=5；

(2)①由翻折可知△PAB≌△PEB，

∴PA=PE， ，

在△DPG和△EFG中

，

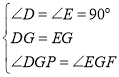∴△DPG≌△EFG，

∴PG=FG，DG=EG，

∴，

∴PE=DF；

②∵，△DPG≌△EFG，AB=8，AD=6，

∴PE=DF=PA，

∴CF=8-DF=8-PA，

∵EF=DP=AD-AP=6-PA，

∴BF=8-EF=8-(6-AP)=2+PA，

在△BCF中，，

∴，

∴,

∴.