题目内容
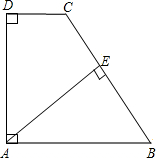
如图，在等腰梯形ABCD中，AB∥CD，AC⊥BC，∠B=60°，BC=2cm，则梯形ABCD的面积为（ ）
| A．6cm2 | B．12cm2 | C．3
| D．6
|
过点C作CE⊥AB于E．
∵AC⊥BC，∠B=60°，
∴∠CAB=30°，
∵BC=2cm，
∴AB=4cm，AC=2
cm，CE=
cm，
∵梯形ABCD是等腰梯形，CD∥AB，
∴∠B=∠DAB=60°，∠CAB=∠DCA=30°，
∴∠DAC=∠DCA=30°，
∴CD=AD=BC=2cm，
∴梯形ABCD的面积=
（AB+CD）×CE=
（4+2）×
=3
cm2．
故选C．
∵AC⊥BC，∠B=60°，∴∠CAB=30°，
∵BC=2cm，
∴AB=4cm，AC=2
| 3 |
| 3 |
∵梯形ABCD是等腰梯形，CD∥AB，
∴∠B=∠DAB=60°，∠CAB=∠DCA=30°，
∴∠DAC=∠DCA=30°，
∴CD=AD=BC=2cm，
∴梯形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选C．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
点P、Q分别从A、C同时出发，设运动时间为t（s）．
