题目内容
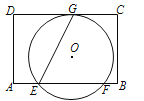
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
【答案】4或12.
【解析】试题分析:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,∴EN=NF,
又∵EG:EF=![]() ,∴EG:EN=
,∴EG:EN=![]() ,
,
又∵GN=AD=8,∴设EN= ![]() ,则GE=
,则GE= ![]() ,
,
根据勾股定理得: ![]() ,解得:x=4,GE=
,解得:x=4,GE=![]() ,
,
设⊙O的半径为![]() ,由
,由![]() ,得:
,得: ![]() ,∴
,∴![]() .∴OK=NB=5,∴EB=9,
.∴OK=NB=5,∴EB=9,
又AE=![]() AB,∴AB=12.
AB,∴AB=12.
同理,当边AD所在的直线与⊙O相切时,AB=4.故答案为:12或4.


练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目