Question

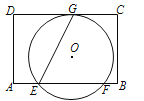
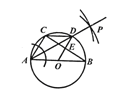
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，AB=8．

（1）利用尺规，作∠CAB的平分线，交⊙O于点D；（保留作图痕迹，不写作法）

（2）在（1）的条件下，连接CD，OD，若AC=CD，求∠B的度数；

（3）在（2）的条件下，OD交BC于点E．求出由线段ED，BE，所围成区域的面积．（其中表示劣弧，结果保留π和根号）

Answer 1

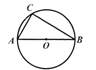
【答案】（1）作图见解析；（2）30°；（3）．

【解析】

试题分析：（1）作AP平分∠CAB交⊙O于D；

（2）由等腰三角形性质得到∠CAD=∠ADC．又由∠ADC=∠B，得到∠CAD=∠B．

再根据角平分线定义得到∠CAD=∠DAB=∠B．由于直径所对圆周角为90°，得到∠ACB=90°，从而得到∠B的度数；

（3）先得到△OEB是30°角的直角三角形，从而得出OE，EB的长，然后把不规则图形面积转化为扇形BOD的面积减去Rt△OEB的面积求解．

试题解析：（1）如图，AP即为所求的∠CAB的平分线；

（2）∵AC=CD，∴∠CAD=∠ADC．又∵∠ADC=∠B，∴∠CAD=∠B．

∵AD平分∠CAB，∴∠CAD=∠DAB=∠B．

∵AB是⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°，∴3∠B=90° ，∴∠B=30°；

（3）由（2）知，∠DAB=30°．又∵∠DOB=2∠DAB，∴∠EOB=60°，∴∠OEB=90°．

在Rt△OEB中，∵OB=4，∠OBE=30°，∴OE=2，BE=，∴S===．