Question

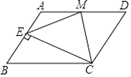
【题目】如图，在平行四边形ABCD中，点M为边AD的中点，过点C作AB的垂线交AB于点E，连接ME，已知AM＝2AE＝4，∠BCE＝30°．

（1）求平行四边形ABCD的面积S；

（2）求证：∠EMC＝2∠AEM．

Answer 1

【答案】（1） ；（2）证明见解析.

【解析】

(1)由AM＝2AE＝4，利用平行四边形的性质可求出BC=AD=8，利用直角三角形的性质得出BE、CE的长,进而得出答案;

(2) 延长EM，CD交于点N，连接CM．通过证明△AEM≌△DNM，可得EM＝MN，然后由直角三角形斜边的中线等于斜边的一半可证MN＝MC，然后根据三角形外角的性质证明即可.

（1）解：∵M为AD的中点，AM＝2AE＝4，

∴AD＝2AM＝8．在ABCD的面积中，BC＝CD＝8，

又∵CE⊥AB，

∴∠BEC＝90°，

∵∠BCE＝30°，

∴BE＝BC＝4，

∴AB＝6，CE＝4，

∴ABCD的面积为：AB×CE＝6×4＝24；

（2）证明：延长EM，CD交于点N，连接CM．

∵在ABCD中，AB∥CD，

∴∠AEM＝∠N，

在△AEM和△DNM中

∵∠AEM=∠N，

AM=DM，

∠AME=∠DMN，

∴△AEM≌△DNM（ASA），

∴EM＝MN，

又∵AB∥CD，CE⊥AB，

∴CE⊥CD，

∴CM是Rt△ECN斜边的中线，

∴MN＝MC，

∴∠N＝∠MCN，

∴∠EMC＝2∠N＝2∠AEM．