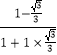题目内容
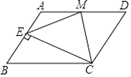
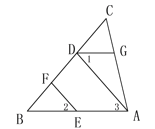
【题目】如图,在![]() 中,
中,![]() 于点E,
于点E,![]() 于点D;点F是AB的中点,连结DF,EF,设
于点D;点F是AB的中点,连结DF,EF,设![]() ,
,![]() ,则
,则![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由直角三角形斜边的中线等于斜边的一半可的AF=DF,BF=EF,从而由等腰三角形的性质得∠ADF=∠DAF,∠EBF=∠BEF,然后根据三角形外角的性质和三角形外角的性质可求得结论.
∵![]() 于点E,
于点E,![]() 于点D;点F是AB的中点,
于点D;点F是AB的中点,
∴AF=DF,BF=EF,
∴∠ADF=∠DAF,∠EBF=∠BEF,
∵∠AFD+∠DFE=∠EBF+∠BEF=2∠EBF,∠BFE+∠DFE=∠DAF+∠ADF=2∠DAF,
∠AFD+∠DFE+∠BFE+∠DFE
=2∠EBF+2∠DAF
=2(∠EBF+∠DAF)
= 2(180°-∠C)
=360°-2∠C,
∴180°+∠DFE=360°-2∠C,
∴180°+x=360°-2y,
∴![]() .
.
故选B.

练习册系列答案
相关题目